Η παρούσα πτυχιακή εργασία στοχεύει στην ανάπτυξη ενός συστήματος πρόβλεψης της θεμελιώδους περιόδου ταλάντωσης πλαισιακών κατασκευών οπλισμένου σκυροδέματος με τοιχοπληρώσεις, αξιοποιώντας τεχνικές μηχανικής μάθησης. Η θεμελιώδης περίοδος αποτελεί κρίσιμη παράμετρο για τον αντισεισμικό σχεδιασμό κατασκευών, καθώς επηρεάζει σημαντικά τις σεισμικές δυνάμεις που αναπτύσσονται στον φορέα [Αστέρης και συν., 2016].
Η εργασία βασίζεται στη βάση δεδομένων FP4026 (Fundamental Period - 4026 cases), η οποία περιλαμβάνει αναλυτικά υπολογισμένες τιμές θεμελιώδους περιόδου για 4026 διαφορετικές περιπτώσεις πλαισίων με τοιχοπληρώσεις. Τα δεδομένα αυτά προέρχονται από παραμετρικές αναλύσεις με το λογισμικό SeismoStruct, σύμφωνα με τα πρότυπα Eurocode 8.
Οι κύριοι στόχοι της εργασίας περιλαμβάνουν την ανάπτυξη μοντέλων μηχανικής μάθησης για την πρόβλεψη της θεμελιώδους περιόδου με βάση γεωμετρικά και μηχανικά χαρακτηριστικά, τη σύγκριση με τις εμπειρικές σχέσεις του Eurocode 8 και την ποσοτικοποίηση της βελτίωσης ακρίβειας, την ανάλυση σημαντικότητας παραμέτρων (feature importance) για την κατανόηση της επίδρασης κάθε μεταβλητής, καθώς και τη δημιουργία εργαλείου πρόβλεψης με γραφική διεπαφή για πρακτική εφαρμογή από μηχανικούς.
Η υλοποίηση επικεντρώνεται σε τέσσερις βασικούς άξονες. Ο πρώτος άξονας αφορά την επεξεργασία δεδομένων FP4026, δηλαδή τη φόρτωση, καθαρισμό και προετοιμασία των δεδομένων για μηχανική μάθηση. Ο δεύτερος άξονας εστιάζει στην ανάπτυξη μοντέλων, περιλαμβάνοντας την εφαρμογή αλγορίθμων όπως Random Forest, Gradient Boosting και Neural Networks, καθώς και τη βελτιστοποίηση υπερπαραμέτρων. Ο τρίτος άξονας αφορά την αξιολόγηση και σύγκριση, με χρήση μετρικών όπως R², MSE και MAE, και σύγκριση με τις κωδικές εξισώσεις. Τέλος, ο τέταρτος άξονας αφορά την τεκμηρίωση και αναπαραγωγιμότητα, με τη δημιουργία οδηγού για την επαλήθευση των αποτελεσμάτων.
Η παρούσα εργασία επικεντρώνεται σε τρία κύρια ερευνητικά ερωτήματα:
Ερώτημα 1: Μπορούν τα μοντέλα μηχανικής μάθησης να προβλέψουν την θεμελιώδη περίοδο με μεγαλύτερη ακρίβεια από τις εμπειρικές σχέσεις του Eurocode 8;
Οι κανονισμοί αντισεισμικού σχεδιασμού (EC8) προτείνουν απλουστευμένες σχέσεις της μορφής:
$$ T_1 = C_t \cdot H^{3/4} $$
οι οποίες δεν λαμβάνουν υπόψη την επίδραση των τοιχοπληρώσεων. Η εργασία θα συγκρίνει την ακρίβεια μοντέλων ML με τις κωδικές εξισώσεις, χρησιμοποιώντας μετρικές όπως R², MSE και MAE.
Ερώτημα 2: Ποιες παράμετροι έχουν τη μεγαλύτερη επίδραση στη θεμελιώδη περίοδο;
Η βάση FP4026 περιλαμβάνει πέντε κύριες μεταβλητές: αριθμό ορόφων, αριθμό ανοιγμάτων, μήκος ανοίγματος, ποσοστό ανοιγμάτων τοιχοποιίας και δυσκαμψία τοιχοποιίας. Μέσω τεχνικών ανάλυσης σημαντικότητας (SHAP, feature importance) θα προσδιοριστεί η σχετική συμβολή κάθε παραμέτρου.
Ερώτημα 3: Ποιος αλγόριθμος μηχανικής μάθησης επιτυγχάνει την καλύτερη απόδοση για το συγκεκριμένο πρόβλημα;
Θα συγκριθούν διαφορετικές προσεγγίσεις (Random Forest, Gradient Boosting, Neural Networks, SVR) ως προς την ακρίβεια πρόβλεψης και την ικανότητα γενίκευσης, με στόχο την επιλογή του βέλτιστου μοντέλου για πρακτική εφαρμογή.
Η μεθοδολογία βασίζεται στην αξιοποίηση της βάσης δεδομένων FP4026 [Αστέρης, 2016], η οποία περιέχει 4026 αναλυτικά υπολογισμένες τιμές θεμελιώδους περιόδου από παραμετρικές αναλύσεις με το λογισμικό SeismoStruct. Τα δεδομένα αυτά αποτελούν το σύνολο εκπαίδευσης και αξιολόγησης των μοντέλων μηχανικής μάθησης.
Η πρώτη φάση περιλαμβάνει τη φόρτωση της βάσης FP4026 από το αρχείο Excel και την εξαγωγή των πέντε μεταβλητών εισόδου, δηλαδή τον αριθμό ορόφων, τον αριθμό ανοιγμάτων, το μήκος ανοίγματος, το ποσοστό ανοιγμάτων τοιχοποιίας και τη δυσκαμψία τοιχοποιίας. Στη συνέχεια πραγματοποιείται κανονικοποίηση και έλεγχος ποιότητας δεδομένων, ενώ τα δεδομένα διαχωρίζονται σε σύνολο εκπαίδευσης (80%) και σύνολο ελέγχου (20%).
Η δεύτερη φάση περιλαμβάνει την εφαρμογή αλγορίθμων μηχανικής μάθησης, συγκεκριμένα Random Forest, Gradient Boosting (LightGBM, XGBoost), Support Vector Regression και Neural Networks. Η βελτιστοποίηση υπερπαραμέτρων πραγματοποιείται με cross-validation (k-fold), ενώ γίνεται ανάλυση σημαντικότητας χαρακτηριστικών με τεχνικές SHAP και feature importance.
Η τρίτη φάση περιλαμβάνει την αξιολόγηση των μοντέλων με μετρικές όπως ο συντελεστής προσδιορισμού R², το MSE, το MAE και το RMSE. Τα αποτελέσματα συγκρίνονται με την εμπειρική σχέση του Eurocode 8:
$$ T_1 = 0.075 \cdot H^{0.75} $$
ενώ πραγματοποιείται οπτικοποίηση των αποτελεσμάτων με scatter plots και residual analysis.
Για την υλοποίηση χρησιμοποιείται η γλώσσα προγραμματισμού Python 3.x με τις βιβλιοθήκες pandas, scikit-learn, XGBoost, LightGBM, matplotlib και SHAP, ενώ η ανάλυση πραγματοποιείται σε Jupyter Notebooks για τη διασφάλιση της αναπαραγωγιμότητας.
Η παρούσα πτυχιακή εργασία οργανώνεται σε δέκα κύρια κεφάλαια, τα οποία ακολουθούν λογική ακολουθία από την θεωρητική θεμελίωση μέχρι την πρακτική υλοποίηση και αξιολόγηση. Το πρώτο κεφάλαιο αποτελεί την εισαγωγή και παρουσιάζει το σκοπό και τους στόχους της εργασίας, ενώ διατυπώνει τα κύρια ερευνητικά ερωτήματα και περιγράφει τη μεθοδολογική προσέγγιση που θα ακολουθηθεί, εξηγώντας παράλληλα τη δομή και την οργάνωση της εργασίας.
Το δεύτερο κεφάλαιο περιλαμβάνει τη βιβλιογραφική ανασκόπηση, η οποία παρουσιάζει το θεωρητικό υπόβαθρο στην ανάλυση κατασκευών, εξετάζει τις υφιστάμενες μεθόδους και τεχνολογίες, επισκοπεί σχετικές έρευνες στον τομέα της τεχνητής νοημοσύνης στην μηχανική, και εκτελεί κριτική ανάλυση της διαθέσιμης βιβλιογραφίας. Στο τρίτο κεφάλαιο αναπτύσσεται η μεθοδολογία, η οποία περιγράφει την ανάλυση απαιτήσεων του συστήματος, παρουσιάζει τον σχεδιασμό της αρχιτεκτονικής συστήματος, τεκμηριώνει την επιλογή εργαλείων και τεχνολογιών, και εξηγεί τη φύση και τα χαρακτηριστικά των δεδομένων.
Το τέταρτο κεφάλαιο εστιάζει στην υλοποίηση, περιγράφοντας τη δημιουργία και διαχείριση της βάσης δεδομένων, εξηγώντας την ανάπτυξη του συστήματος εξαγωγής χαρακτηριστικών, παρουσιάζοντας τη δημιουργία φορέα και την ανάλυση αποτελεσμάτων, και τεκμηριώνοντας τη διαδικασία ελέγχου και επικύρωσης. Το πέμπτο κεφάλαιο ασχολείται με την ανάλυση με τεχνητή νοημοσύνη, περιγράφοντας τους επιλεγμένους αλγορίθμους και την αρχιτεκτονική AI, εκτελώντας ποσοτικοποίηση της ανάλυσης δεδομένων, αναλύοντας τις σχέσεις μεταξύ εισόδων και εξόδων, και προσδιορίζοντας την ιεράρχηση σημασίας των μεταβλητών εισόδου.
Το έκτο κεφάλαιο παρουσιάζει τα αποτελέσματα με πίνακες και διαγράμματα, περιλαμβάνει παραδείγματα εφαρμογής σε πραγματικά σενάρια, και εκτελεί συζήτηση και ερμηνεία των αποτελεσμάτων. Το έβδομο κεφάλαιο συνοψίζει τα κύρια συμπεράσματα της έρευνας, προτείνει κατευθύνσεις για μελλοντική έρευνα, και προτείνει βελτιώσεις και δυνητικές επεκτάσεις.
Το όγδοο κεφάλαιο λειτουργεί ως οδηγός αναπαραγωγής αποτελεσμάτων, περιγράφοντας τις απαιτήσεις συστήματος για εγκατάσταση, παρέχοντας λεπτομερείς οδηγίες εγκατάστασης και εκτέλεσης, και συμπεριλαμβάνοντας παραδείγματα για αναπαραγωγή των αποτελεσμάτων. Το ένατο κεφάλαιο περιλαμβάνει τα παραρτήματα και παρέχει τον πλήρη κώδικα υλοποίησης, περιέχει πρόσθετα διαγράμματα και πίνακες, και τεκμηριώνει API και εργαλεία που χρησιμοποιήθηκαν. Το δέκατο κεφάλαιο αποτελεί τη βιβλιογραφία και καταγράφει όλες τις πηγές που χρησιμοποιήθηκαν στην έρευνα, ακολουθώντας συγκεκριμένη μορφή παραπομπών.
Η δομή αυτή επιτρέπει τη σταδιακή παρουσίαση της έρευνας, ξεκινώντας από τη θεωρητική θεμελίωση και προχωρώντας στην πρακτική εφαρμογή και αξιολόγηση, διασφαλίζοντας τη συνοχή και την επιστημονική αυστηρότητα της εργασίας.
Η θεμελιώδης περίοδος ταλάντωσης (fundamental period of vibration) αποτελεί μία από τις κρισιμότερες παραμέτρους για τον αντισεισμικό σχεδιασμό κατασκευών, καθώς επηρεάζει σημαντικά την καταστροφική επίδραση των σεισμικών δυνάμεων [Αστέρης και συν., 2015, 2016]. Η ακριβής εκτίμηση της θεμελιώδους περιόδου είναι απαραίτητη για την αξιόπιστη ανάλυση και τον σχεδιασμό πλαισιακών φορέων από οπλισμένο σκυρόδεμα με τοιχοπληρώσεις τοιχοποιίας.
Στην πράξη, οι κανονισμοί αντισεισμικού σχεδιασμού (όπως ο Eurocode 8) παρέχουν απλουστευμένες εμπειρικές σχέσεις για τον υπολογισμό της θεμελιώδους περιόδου. Ωστόσο, αυτές οι σχέσεις συχνά δεν λαμβάνουν πλήρως υπόψη την επίδραση των τοιχοπληρώσεων τοιχοποιίας, οι οποίες δύνανται να μεταβάλουν σημαντικά τη δυναμική συμπεριφορά του φορέα [Αστέρης & Cavaleri, 2016]. Η παρουσία τοιχοπληρώσεων αυξάνει τη δυσκαμψία του συστήματος και μειώνει την περίοδο ταλάντωσης, ενώ τα ανοίγματα (κουφώματα θυρών και παραθύρων) επηρεάζουν επίσης τη δυναμική συμπεριφορά.
Σύμφωνα με την εκτενή έρευνα του Παναγιώτη Αστέρη και των συνεργατών του [Αστέρης και συν., 2015, 2016], οι κύριες παράμετροι που επηρεάζουν τη θεμελιώδη περίοδο ταλάντωσης των πλαισιακών κατασκευών από οπλισμένο σκυρόδεμα με τοιχοπληρώσεις είναι:
Στη βάση δεδομένων FP4026, το σύνολο των κατασκευών σχεδιάστηκε σύμφωνα με τις διατάξεις του Ευρωκώδικα 8 με τις ακόλουθες παραμέτρους υλικών [Αστέρης, 2016]:
| Παράμετρος | Τιμή |
|---|---|
| Αντοχή σκυροδέματος | 25.00 MPa (C25/30) |
| Μέτρο ελαστικότητας σκυροδέματος | 31.00 GPa |
| Όριο διαρροής χάλυβα | 500.00 MPa (B500c) |
| Διαστάσεις δοκών | 250/600 mm |
| Πάχος πλάκας | 150 mm |
| Μόνιμα φορτία | 1.50 + 0.90 kN/m² |
| Κινητά φορτία | 3.50 kN/m² |
Οι διατομές υποστυλωμάτων είναι τετραγωνικές και μεταβάλλονται ανάλογα με τον αριθμό ορόφων και το μήκος ανοίγματος, με ποσοστό οπλισμού μεταξύ 1.0% και 1.5%.
Από τις πρώτες προσπάθειες μοντελοποίησης της απόκρισης σύνθετων κατασκευών πλαισίου με τοιχοπληρώσεις, οι πειραματικές και εννοιολογικές παρατηρήσεις έχουν δείξει ότι ένας διαγώνιος ελκυστήρας με κατάλληλα γεωμετρικά και μηχανικά χαρακτηριστικά μπορεί να παρέχει μια λύση στο πρόβλημα [Crisafulli & Carr, 2007].
Ο Αστέρης [2003, 2008] ανέπτυξε μια μεθοδολογία πεπερασμένων στοιχείων για την εκτίμηση των μηκών επαφής μεταξύ τοιχοποιίας και πλαισιακού φορέα, η οποία έχει χρησιμοποιηθεί για τη διερεύνηση της επίδρασης των ανοιγμάτων στην πλευρική δυσκαμψία των πανέλων τοιχοποιίας. Βάσει των ευρημάτων αυτών, προτάθηκε και υλοποιήθηκε η ακόλουθη αναλυτική σχέση για τον συντελεστή μείωσης δυσκαμψίας της τοιχοποιίας $\lambda$:
$$ \lambda = 1 - 2.53 \sqrt{\frac{A_{open}}{A_{infill}}} + 3.03 \frac{A_{open}}{A_{infill}} $$
όπου $\frac{A_{open}}{A_{infill}}$ είναι ο λόγος της επιφάνειας ανοίγματος προς την επιφάνεια της τοιχοποιίας.
Στις αναλύσεις που πραγματοποιήθηκαν με το λογισμικό SeismoStruct [SeismoSoft], οι τοιχοπληρώσεις τοιχοποιίας μοντελοποιήθηκαν χρησιμοποιώντας ένα μη γραμμικό κυκλικό μοντέλο ισοδύναμου ελκυστήρα που προτάθηκε από τους Crisafulli και Carr [2007].
Η βάση δεδομένων FP4026 (Fundamental Period - 4026 περιπτώσεις πλαισίων με τοιχοπληρώσεις) δημοσιεύθηκε από τον καθηγητή Παναγιώτη Γ. Αστέρη του Εργαστηρίου Υπολογιστικής Μηχανικής, Τμήμα Πολιτικών Μηχανικών, Ανώτατη Σχολή Παιδαγωγικής και Τεχνολογικής Εκπαίδευσης (ΑΣΠΑΙΤΕ), Αθήνα [Αστέρης, 2016] και αποτελεί μια εκτενή συλλογή αναλυτικά προσδιορισμένων τιμών της θεμελιώδους περιόδου για πλαισιακές κατασκευές από οπλισμένο σκυρόδεμα με τοιχοπληρώσεις τοιχοποιίας. Η βάση περιλαμβάνει:
Όλα τα πλαίσια σχεδιάστηκαν σύμφωνα με τα πρότυπα Eurocode 8 [EN 1998-1:2004] για σεισμική ζώνη Ι με επιτάχυνση αναφοράς 0.16g, σκυρόδεμα κατηγορίας C25/30, χάλυβα οπλισμού B500c, και συντελεστή συμπεριφοράς q=3.45 (μέτρια πλαστιμότητα DCM).
Πρόσφατες έρευνες έχουν επικεντρωθεί στη χρήση τεχνικών μηχανικής μάθησης για την πρόβλεψη της θεμελιώδους περιόδου πλαισιακών κατασκευών με τοιχοπληρώσεις, αξιοποιώντας τη βάση δεδομένων FP4026 και παρόμοια datasets:
Ο Αστέρης και οι συνεργάτες του [2016] εφάρμοσαν τεχνητά νευρωνικά δίκτυα (Artificial Neural Networks, ANN) για την πρόβλεψη της θεμελιώδους περιόδου. Τα αποτελέσματα κατέδειξαν ότι τα ΑΝΝ δύνανται να προβλέψουν με υψηλή ακρίβεια την περίοδο ταλάντωσης λαμβάνοντας υπόψη τις πέντε κύριες παραμέτρους (αριθμός ορόφων, αριθμός ανοιγμάτων, μήκος ανοίγματος, ποσοστό ανοιγμάτων τοιχοποιίας, δυσκαμψία τοιχοποιίας).
Πρόσφατες μελέτες [2023] έχουν εφαρμόσει προηγμένες τεχνικές όπως:
Πρόσφατα, οι ερευνητές [2023] έχουν ενσωματώσει τεχνικές ερμηνευσιμότητας όπως:
Τα αποτελέσματα δείχνουν ότι το ποσοστό ανοιγμάτων είναι η πιο επιδραστική παράμετρος, ακολουθούμενη από τον αριθμό ορόφων και τη δυσκαμψία τοιχοποιίας.
Οι εμπειρικές σχέσεις που προτείνονται από κανονισμούς (π.χ. Eurocode 8: $T_1 = C_t \cdot H^{3/4}$, όπου $C_t = 0.075$ για πλαίσια Ο/Σ και $H$ το ύψος σε μέτρα) τείνουν να υπερεκτιμούν την περίοδο για κατασκευές με πλήρεις τοιχοπληρώσεις και να την υποεκτιμούν για γυμνά πλαίσια.
Μελέτες που χρησιμοποιούν τη βάση FP4026 [2020, 2022] έχουν δείξει ότι τα μοντέλα μηχανικής μάθησης υπερτερούν σημαντικά των κωδικών εξισώσεων, επιτυγχάνοντας συντελεστές προσδιορισμού $R^2 > 0.95$ και μέσα σφάλματα $< 5\%$.
Η ανασκόπηση της βιβλιογραφίας αναδεικνύει τη σημασία της ακριβούς εκτίμησης της θεμελιώδους περιόδου για τον αντισεισμικό σχεδιασμό, την πολυπλοκότητα της επίδρασης των τοιχοπληρώσεων που εξαρτάται από πολλές παραμέτρους, την αξία μεγάλων αναλυτικών βάσεων δεδομένων όπως η FP4026 για την ανάπτυξη προβλεπτικών μοντέλων, το δυναμικό των τεχνικών μηχανικής μάθησης να παρέχουν ακριβέστερες προβλέψεις από τις εμπειρικές σχέσεις των κανονισμών, καθώς και τη σημασία της ερμηνευσιμότητας των μοντέλων για την κατανόηση των φυσικών μηχανισμών και την αποδοχή από τη μηχανική κοινότητα.
Η βάση δεδομένων FP4026 (Fundamental Period - 4026 cases) αποτελεί το θεμέλιο της παρούσας έρευνας και δημοσιεύθηκε από τον Παναγιώτη Αστέρη [2016] ως συμπληρωματικό υλικό επιστημονικής δημοσίευσης στο περιοδικό Data in Brief. Τα δεδομένα προέρχονται από εκτεταμένες παραμετρικές αναλύσεις που πραγματοποιήθηκαν με το λογισμικό πεπεραμένων στοιχείων SeismoStruct, το οποίο είναι ευρέως αποδεκτό στην επιστημονική κοινότητα για τη μη γραμμική ανάλυση κατασκευών. Η βάση περιλαμβάνει 4026 διαφορετικές περιπτώσεις επίπεδων πλαισίων οπλισμένου σκυροδέματος με τοιχοπληρώσεις τοιχοποιίας, καλύπτοντας ένα ευρύ φάσμα γεωμετρικών και μηχανικών παραμέτρων. Όλα τα πλαίσια σχεδιάστηκαν σύμφωνα με τις απαιτήσεις του Ευρωκώδικα 8 (EN 1998-1:2004), διασφαλίζοντας τη συμβατότητα με τις σύγχρονες πρακτικές αντισεισμικού σχεδιασμού.
Η βάση δεδομένων περιλαμβάνει πέντε μεταβλητές εισόδου (ανεξάρτητες μεταβλητές) και μία μεταβλητή εξόδου (εξαρτημένη μεταβλητή). Η πρώτη μεταβλητή εισόδου είναι ο αριθμός ορόφων, ο οποίος κυμαίνεται από 1 έως 22 με βήμα μονάδας, καθορίζοντας το συνολικό ύψος της κατασκευής δεδομένου ότι το ύψος ορόφου είναι σταθερό και ίσο με 3.0 m. Η δεύτερη μεταβλητή είναι ο αριθμός ανοιγμάτων του πλαισίου, ο οποίος λαμβάνει τιμές 2, 4 ή 6, επηρεάζοντας τη συνολική δυσκαμψία και την κατανομή μάζας του φορέα. Η τρίτη μεταβλητή είναι το μήκος ανοίγματος (απόσταση μεταξύ αξόνων υποστυλωμάτων), το οποίο λαμβάνει τέσσερις διακριτές τιμές: 3.0 m, 4.5 m, 6.0 m και 7.5 m. Η τέταρτη μεταβλητή είναι το ποσοστό ανοιγμάτων στην τοιχοποιία, το οποίο εκφράζεται ως ποσοστό της επιφάνειας του πανέλου τοιχοποιίας και λαμβάνει τιμές 0% (πλήρης τοιχοπλήρωση), 25%, 50%, 75% και 100% (γυμνό πλαίσιο χωρίς τοιχοπλήρωση). Η πέμπτη μεταβλητή είναι η δυσκαμψία της τοιχοποιίας, η οποία εκφράζεται σε μονάδες 10⁵ kN/m και λαμβάνει επτά διαφορετικές τιμές (2.25, 4.50, 7.50, 11.25, 15.00, 20.00, 25.00), αντιπροσωπεύοντας διαφορετικούς συνδυασμούς μέτρου ελαστικότητας και πάχους τοιχοποιίας. Η μεταβλητή εξόδου είναι η θεμελιώδης περίοδος ταλάντωσης T, εκφρασμένη σε δευτερόλεπτα (sec), η οποία υπολογίστηκε αναλυτικά μέσω ιδιομορφικής ανάλυσης με το λογισμικό SeismoStruct.
Η προεπεξεργασία των δεδομένων αποτελεί κρίσιμο στάδιο για την επιτυχή εφαρμογή αλγορίθμων μηχανικής μάθησης. Αρχικά πραγματοποιείται έλεγχος για ελλείπουσες τιμές (missing values) και ακραίες τιμές (outliers), αν και η βάση FP4026 προέρχεται από αναλυτικούς υπολογισμούς και δεν αναμένονται τέτοια προβλήματα. Στη συνέχεια εφαρμόζεται κανονικοποίηση (normalization) των μεταβλητών εισόδου, η οποία είναι απαραίτητη για την αποφυγή προβλημάτων κλίμακας κατά την εκπαίδευση των μοντέλων. Στην παρούσα εργασία χρησιμοποιείται ο MaxAbsScaler της βιβλιοθήκης scikit-learn, ο οποίος κλιμακώνει κάθε χαρακτηριστικό διαιρώντας με τη μέγιστη απόλυτη τιμή του, διατηρώντας έτσι τα μηδενικά στα αραιά δεδομένα και τη διασπορά των τιμών.
Ο διαχωρισμός των δεδομένων σε σύνολο εκπαίδευσης (training set) και σύνολο ελέγχου (test set) αποτελεί θεμελιώδες βήμα για την αξιολόγηση της ικανότητας γενίκευσης των μοντέλων μηχανικής μάθησης. Στην παρούσα εργασία εξετάζονται τρεις διαφορετικές στρατηγικές διαχωρισμού. Η πρώτη στρατηγική είναι ο απλός τυχαίος διαχωρισμός (train_test_split), κατά τον οποίο τα δεδομένα χωρίζονται τυχαία σε δύο υποσύνολα με καθορισμένη αναλογία, συνήθως 80% για εκπαίδευση και 20% για έλεγχο. Η δεύτερη στρατηγική είναι η K-Fold Cross Validation, κατά την οποία τα δεδομένα χωρίζονται σε K ίσα υποσύνολα (folds) και η εκπαίδευση επαναλαμβάνεται K φορές, χρησιμοποιώντας κάθε φορά διαφορετικό fold ως σύνολο ελέγχου. Η τρίτη στρατηγική είναι το ShuffleSplit, το οποίο συνδυάζει τα πλεονεκτήματα των δύο προηγούμενων μεθόδων, πραγματοποιώντας πολλαπλούς τυχαίους διαχωρισμούς και υπολογίζοντας τη μέση απόδοση. Στην παρούσα υλοποίηση χρησιμοποιείται η μέθοδος ShuffleSplit με 5 επαναλήψεις και ποσοστό ελέγχου 10%, παρέχοντας μια ισορροπία μεταξύ υπολογιστικού κόστους και αξιοπιστίας εκτίμησης.
Η κανονικοποίηση των χαρακτηριστικών εισόδου είναι απαραίτητη για τη βελτίωση της σύγκλισης και της σταθερότητας των αλγορίθμων μηχανικής μάθησης, ιδιαίτερα για τα νευρωνικά δίκτυα και τις μεθόδους βασισμένες σε απόσταση. Διάφορες τεχνικές κανονικοποίησης είναι διαθέσιμες, καθεμία με συγκεκριμένα πλεονεκτήματα. Ο StandardScaler μετασχηματίζει τα δεδομένα ώστε να έχουν μέση τιμή μηδέν και τυπική απόκλιση μονάδα, και είναι κατάλληλος για δεδομένα με κανονική κατανομή. Ο MinMaxScaler κλιμακώνει τα δεδομένα στο διάστημα [0,1], διατηρώντας τη σχετική απόσταση μεταξύ τιμών. Ο MaxAbsScaler κλιμακώνει κάθε χαρακτηριστικό διαιρώντας με τη μέγιστη απόλυτη τιμή, με αποτέλεσμα τιμές στο διάστημα [-1,1], και είναι κατάλληλος για αραιά δεδομένα καθώς διατηρεί τα μηδενικά. Ο RobustScaler χρησιμοποιεί τη διάμεσο και το ενδοτεταρτημοριακό εύρος, καθιστώντας τον ανθεκτικό σε ακραίες τιμές. Στην παρούσα εργασία επιλέγεται ο MaxAbsScaler λόγω της ικανότητάς του να διατηρεί τη δομή των δεδομένων και να αποφεύγει προβλήματα με μηδενικές τιμές.
Ο αλγόριθμος Random Forest αποτελεί μια μέθοδο ensemble learning που συνδυάζει πολλαπλά δέντρα απόφασης (decision trees) για τη βελτίωση της ακρίβειας πρόβλεψης και τη μείωση της υπερπροσαρμογής (overfitting). Κάθε δέντρο εκπαιδεύεται σε ένα τυχαίο υποσύνολο των δεδομένων εκπαίδευσης (bootstrap sampling) και χρησιμοποιεί ένα τυχαίο υποσύνολο χαρακτηριστικών σε κάθε διάσπαση, εισάγοντας ποικιλομορφία στα επιμέρους δέντρα. Η τελική πρόβλεψη προκύπτει ως ο μέσος όρος των προβλέψεων όλων των δέντρων (για προβλήματα παλινδρόμησης). Τα κύρια πλεονεκτήματα του Random Forest περιλαμβάνουν την υψηλή ακρίβεια, την ανθεκτικότητα σε θόρυβο και ακραίες τιμές, την ικανότητα χειρισμού μη γραμμικών σχέσεων, και τη δυνατότητα εκτίμησης της σημαντικότητας των χαρακτηριστικών (feature importance).
graph TD
A[Σύνολο δεδομένων **FP4026**
N=4026 περιπτώσεις] --> B1[Bootstrap Sample 1
Τυχαίο υποσύνολο δεδομένων]
A --> B2[Bootstrap Sample 2
Τυχαίο υποσύνολο δεδομένων]
A --> B3[Bootstrap Sample 3
Τυχαίο υποσύνολο δεδομένων]
A --> B4[... Bootstrap Sample n
Τυχαίο υποσύνολο δεδομένων]
B1 --> T1[Δέντρο Απόφασης 1
Τυχαία χαρακτηριστικά σε κάθε κόμβο]
B2 --> T2[Δέντρο Απόφασης 2
Τυχαία χαρακτηριστικά σε κάθε κόμβο]
B3 --> T3[Δέντρο Απόφασης 3
Τυχαία χαρακτηριστικά σε κάθε κόμβο]
B4 --> T4[Δέντρο Απόφασης n
Τυχαία χαρακτηριστικά σε κάθε κόμβο]
T1 --> P1[Πρόβλεψη T₁]
T2 --> P2[Πρόβλεψη T₂]
T3 --> P3[Πρόβλεψη T₃]
T4 --> P4[Πρόβλεψη Tₙ]
P1 --> F[Τελική Πρόβλεψη
T = mean T₁, T₂, ..., Tₙ]
P2 --> F
P3 --> F
P4 --> F
F --> O[Θεμελιώδης Περίοδος T sec]
style A fill:#e1f5ff
style F fill:#ffe1e1
style O fill:#e1ffe1
Σχήμα 3.1: Διαδικασία πρόβλεψης με τον αλγόριθμο Random Forest. Τα δεδομένα εκπαίδευσης υποβάλλονται σε bootstrap sampling για τη δημιουργία πολλαπλών υποσυνόλων. Κάθε δέντρο απόφασης εκπαιδεύεται ανεξάρτητα με τυχαία επιλογή χαρακτηριστικών σε κάθε διάσπαση κόμβου. Η τελική πρόβλεψη προκύπτει από τον μέσο όρο των επιμέρους προβλέψεων, μειώνοντας τη διακύμανση και την υπερπροσαρμογή του μοντέλου.
Ο αλγόριθμος Gradient Boosting είναι μια επαναληπτική μέθοδος ensemble που χτίζει μοντέλα διαδοχικά, με κάθε νέο μοντέλο να προσπαθεί να διορθώσει τα σφάλματα των προηγούμενων. Σε αντίθεση με το Random Forest που εκπαιδεύει τα δέντρα παράλληλα, το Gradient Boosting εκπαιδεύει κάθε δέντρο στα υπόλοιπα (residuals) του προηγούμενου μοντέλου, ελαχιστοποιώντας μια συνάρτηση απώλειας μέσω της μεθόδου gradient descent. Πρόσφατες υλοποιήσεις όπως οι XGBoost και LightGBM έχουν βελτιώσει σημαντικά την υπολογιστική αποδοτικότητα και την ακρίβεια του αλγορίθμου.
graph TB
subgraph row1[" "]
direction LR
subgraph Αρχικοποίηση
D0[Δεδομένα FP4026] --> M0[Μοντέλο M₀
Μέση τιμή T̄]
end
subgraph Επανάληψη_1[Επανάληψη 1]
R1[Υπόλοιπα
r₁ = y - T̄] --> T1[Δέντρο 1]
T1 --> U1[F₁ = F₀ + α·Tree₁]
end
end
subgraph row2[" "]
direction LR
subgraph Επανάληψη_2[Επανάληψη 2]
R2[Υπόλοιπα
r₂ = y - F₁] --> T2[Δέντρο 2]
T2 --> U2[F₂ = F₁ + α·Tree₂]
end
subgraph Τελικό_Μοντέλο[Τελικό Μοντέλο]
DOTS[... n επαναλήψεις ...] --> Final[F = F₀ + α·Σ Treeᵢ]
Final --> Pred[Πρόβλεψη
Περίοδος T]
end
end
M0 --> R1
U1 --> R2
U2 --> DOTS
style D0 fill:#e1f5ff
style M0 fill:#fff4e1
style T1 fill:#d4edda
style T2 fill:#d4edda
style Final fill:#ffe1e1
style Pred fill:#e1ffe1
Σχήμα 3.2: Διαδικασία επαναληπτικής εκπαίδευσης Gradient Boosting. Κάθε νέο δέντρο εκπαιδεύεται στα υπόλοιπα (residuals) του προηγούμενου μοντέλου, διορθώνοντας σταδιακά τα σφάλματα. Ο συντελεστής μάθησης α ελέγχει τη συμβολή κάθε δέντρου στο τελικό μοντέλο. Η διαδικασία συνεχίζεται μέχρι να επιτευχθεί η επιθυμητή ακρίβεια ή να συμπληρωθεί ο καθορισμένος αριθμός δέντρων.
Τα τεχνητά νευρωνικά δίκτυα πολλαπλών επιπέδων (Multilayer Perceptron - MLP) αποτελούν μια κλάση feedforward νευρωνικών δικτύων που περιλαμβάνουν ένα επίπεδο εισόδου, ένα ή περισσότερα κρυφά επίπεδα και ένα επίπεδο εξόδου. Κάθε νευρώνας υπολογίζει ένα σταθμισμένο άθροισμα των εισόδων του και εφαρμόζει μια μη γραμμική συνάρτηση ενεργοποίησης. Η εκπαίδευση πραγματοποιείται μέσω του αλγορίθμου οπισθοδιάδοσης (backpropagation) σε συνδυασμό με μεθόδους βελτιστοποίησης όπως ο Adam (Adaptive Moment Estimation). Στην παρούσα υλοποίηση χρησιμοποιείται η βιβλιοθήκη PyTorch για την κατασκευή νευρωνικών δικτύων με παραμετροποιήσιμο αριθμό κρυφών επιπέδων, αριθμό νευρώνων ανά επίπεδο και συνάρτηση ενεργοποίησης. Οι διαθέσιμες συναρτήσεις ενεργοποίησης περιλαμβάνουν τη ReLU (Rectified Linear Unit) που ορίζεται ως $f(x) = \max(0, x)$, τη Tanh (υπερβολική εφαπτομένη) με τιμές στο διάστημα (-1, 1), τη Sigmoid με τιμές στο διάστημα (0, 1), και τη LeakyReLU που επιτρέπει μικρή κλίση για αρνητικές τιμές αποφεύγοντας το πρόβλημα του «νεκρού ReLU».
graph LR
I1[Αριθμός ορόφων] --> H1_1((N₁))
I2[Αριθμός ανοιγμάτων] --> H1_1
I3[Μήκος ανοίγματος] --> H1_1
I4[Ποσοστό ανοιγμάτων %] --> H1_1
I5[Δυσκαμψία τοιχοποιίας] --> H1_1
I1 --> H1_2((N₂))
I2 --> H1_2
I3 --> H1_2
I4 --> H1_2
I5 --> H1_2
I1 --> H1_3((N₃))
I2 --> H1_3
I3 --> H1_3
I4 --> H1_3
I5 --> H1_3
H1_1 --> H2_1((N₁))
H1_2 --> H2_1
H1_3 --> H2_1
H1_1 --> H2_2((N₂))
H1_2 --> H2_2
H1_3 --> H2_2
H1_1 --> H2_3((N₃))
H1_2 --> H2_3
H1_3 --> H2_3
H2_1 --> OUT((T))
H2_2 --> OUT
H2_3 --> OUT
OUT --> Result[Θεμελιώδης Περίοδος
T sec]
style I1 fill:#e1f5ff
style I2 fill:#e1f5ff
style I3 fill:#e1f5ff
style I4 fill:#e1f5ff
style I5 fill:#e1f5ff
style H1_1 fill:#fff4e1
style H1_2 fill:#fff4e1
style H1_3 fill:#fff4e1
style H2_1 fill:#ffe1e1
style H2_2 fill:#ffe1e1
style H2_3 fill:#ffe1e1
style OUT fill:#e1ffe1
style Result fill:#d4edda
Σχήμα 3.3: Αρχιτεκτονική νευρωνικού δικτύου MLP για την πρόβλεψη της θεμελιώδους περιόδου. Το δίκτυο αποτελείται από επίπεδο εισόδου με 5 νευρώνες (μία για κάθε μεταβλητή), δύο κρυφά επίπεδα με 3 νευρώνες το καθένα και συνάρτηση ενεργοποίησης ReLU, και επίπεδο εξόδου με 1 νευρώνα για την πρόβλεψη της περιόδου T. Η εκπαίδευση πραγματοποιείται με τον αλγόριθμο Adam optimizer και συνάρτηση απώλειας MSE για 1000 epochs.
Η Support Vector Regression αποτελεί επέκταση των Support Vector Machines για προβλήματα παλινδρόμησης. Ο αλγόριθμος προσπαθεί να βρει μια συνάρτηση που έχει απόκλιση το πολύ ε από τις πραγματικές τιμές για όλα τα δεδομένα εκπαίδευσης, ενώ ταυτόχρονα είναι όσο το δυνατόν πιο «επίπεδη». Η χρήση συναρτήσεων πυρήνα (kernel functions) επιτρέπει τον χειρισμό μη γραμμικών σχέσεων μεταξύ των μεταβλητών.
graph LR
IN["Είσοδος
x₁, x₂, x₃, x₄, x₅"] --> K["Kernel Function
φ: x → υψηλή διάσταση"]
K --> HP["Υπερεπίπεδο
f(x) = w·φ(x) + b"]
HP --> ET["ε-Σωλήνας
|y - f(x)| ≤ ε"]
ET --> SV["Support Vectors
Σημεία εκτός σωλήνα"]
SV --> OPT["Βελτιστοποίηση
min ½||w||² + C·Σξᵢ"]
OPT --> PRED["Πρόβλεψη
Περίοδος T"]
style IN fill:#e1f5ff
style K fill:#fff4e1
style HP fill:#ffe1e1
style ET fill:#ffeaa7
style SV fill:#dfe6e9
style OPT fill:#fab1a0
style PRED fill:#e1ffe1
Σχήμα 3.4: Διαδικασία Support Vector Regression. Τα δεδομένα εισόδου μετασχηματίζονται μέσω συνάρτησης kernel σε υψηλότερη διάσταση. Η μέθοδος αναζητεί υπερεπίπεδο παλινδρόμησης που βρίσκεται εντός ε-σωλήνα από τις πραγματικές τιμές. Τα σημεία εκτός του σωλήνα (support vectors) καθορίζουν το μοντέλο. Η παράμετρος C ελέγχει την ισορροπία μεταξύ επιπεδότητας και ανοχής σφαλμάτων.
Εκτός από τους παραπάνω αλγορίθμους, η υλοποίηση υποστηρίζει και άλλες μεθόδους παλινδρόμησης όπως ο K-Nearest Neighbors (KNN) που βασίζεται στην εγγύτητα με γνωστά παραδείγματα, η Ridge Regression που εισάγει κανονικοποίηση L2 για τον έλεγχο της πολυπλοκότητας του μοντέλου, η Lasso Regression που χρησιμοποιεί κανονικοποίηση L1 επιτρέποντας επιλογή χαρακτηριστικών, και η ElasticNet που συνδυάζει τις κανονικοποιήσεις L1 και L2.
Η μέθοδος SHAP (SHapley Additive exPlanations) βασίζεται στις τιμές Shapley από τη θεωρία παιγνίων και παρέχει ένα ενοποιημένο πλαίσιο για την ερμηνεία προβλέψεων μοντέλων μηχανικής μάθησης [Lundberg & Lee, 2017]. Η τιμή SHAP κάθε χαρακτηριστικού αντιπροσωπεύει τη συμβολή του στη διαφορά μεταξύ της πρόβλεψης για ένα συγκεκριμένο δείγμα και της μέσης πρόβλεψης του μοντέλου. Οι τιμές SHAP ικανοποιούν σημαντικές ιδιότητες όπως η τοπική ακρίβεια (το άθροισμα των τιμών SHAP ισούται με τη διαφορά μεταξύ πρόβλεψης και μέσης τιμής), η συνέπεια (αν ένα χαρακτηριστικό συμβάλλει περισσότερο σε ένα μοντέλο, η τιμή SHAP του πρέπει να είναι μεγαλύτερη), και η μηδενική συμβολή (χαρακτηριστικά που δεν επηρεάζουν την πρόβλεψη έχουν μηδενική τιμή SHAP).
Στην παρούσα εργασία χρησιμοποιείται ο KernelExplainer της βιβλιοθήκης shap, ο οποίος είναι μια model-agnostic μέθοδος που μπορεί να εφαρμοστεί σε οποιοδήποτε μοντέλο. Ο KernelExplainer προσεγγίζει τις τιμές SHAP χρησιμοποιώντας μια σταθμισμένη γραμμική παλινδρόμηση με ειδικά σχεδιασμένα βάρη που προκύπτουν από τη θεωρία Shapley. Η ανάλυση μπορεί να εφαρμοστεί είτε στο σύνολο των δεδομένων είτε σε ένα αντιπροσωπευτικό υποσύνολο, ανάλογα με το υπολογιστικό κόστος. Τα αποτελέσματα οπτικοποιούνται μέσω διαγραμμάτων violin που δείχνουν την κατανομή των τιμών SHAP για κάθε χαρακτηριστικό, καθώς και μέσω διαγραμμάτων bar που παρουσιάζουν τη μέση απόλυτη τιμή SHAP, αντιπροσωπεύοντας τη συνολική σημαντικότητα κάθε χαρακτηριστικού.
Ο συντελεστής προσδιορισμού $R^2$ (coefficient of determination) αποτελεί τη βασική μετρική αξιολόγησης της ικανότητας πρόβλεψης των μοντέλων παλινδρόμησης. Ορίζεται ως η αναλογία της διακύμανσης της εξαρτημένης μεταβλητής που εξηγείται από το μοντέλο και υπολογίζεται από τον τύπο:
$$R^2 = 1 - \frac{SS_{res}}{SS_{tot}}$$
όπου $SS_{res}$ είναι το άθροισμα τετραγώνων των υπολοίπων (sum of squared residuals) και $SS_{tot}$ το συνολικό άθροισμα τετραγώνων (total sum of squares). Ο $R^2$ λαμβάνει τιμές από $-\infty$ έως $1$, όπου η τιμή $1$ υποδηλώνει τέλεια προσαρμογή, η τιμή $0$ υποδηλώνει ότι το μοντέλο εξηγεί την ίδια διακύμανση με τον μέσο όρο, και αρνητικές τιμές υποδηλώνουν χειρότερη απόδοση από τον μέσο όρο.
Το μέσο τετραγωνικό σφάλμα (Mean Squared Error - MSE) υπολογίζεται ως ο μέσος όρος των τετραγώνων των διαφορών μεταξύ προβλεπόμενων και πραγματικών τιμών. Η ρίζα του MSE (Root Mean Squared Error - RMSE) έχει το πλεονέκτημα ότι εκφράζεται στις ίδιες μονάδες με την εξαρτημένη μεταβλητή, διευκολύνοντας την ερμηνεία. Και οι δύο μετρικές δίνουν μεγαλύτερη βαρύτητα στα μεγάλα σφάλματα λόγω της τετραγωνικής συνάρτησης.
Το μέσο απόλυτο σφάλμα (Mean Absolute Error - MAE) υπολογίζεται ως ο μέσος όρος των απόλυτων τιμών των διαφορών μεταξύ προβλεπόμενων και πραγματικών τιμών. Σε αντίθεση με το MSE, το MAE είναι λιγότερο ευαίσθητο σε ακραίες τιμές και παρέχει μια πιο «δίκαιη» εικόνα του τυπικού σφάλματος πρόβλεψης.
Ο Eurocode 8 (EN 1998-1:2004) προτείνει την ακόλουθη απλουστευμένη σχέση για τον υπολογισμό της θεμελιώδους περιόδου ταλάντωσης κτιρίων:
$$T_1 = C_t \cdot H^{3/4}$$
όπου T₁ η θεμελιώδης περίοδος σε δευτερόλεπτα, H το συνολικό ύψος του κτιρίου σε μέτρα, και Ct συντελεστής που εξαρτάται από τον τύπο του φορέα. Για πλαισιακές κατασκευές οπλισμένου σκυροδέματος η τιμή του Ct είναι 0.075. Η σχέση αυτή δεν λαμβάνει υπόψη την επίδραση των τοιχοπληρώσεων, γεγονός που οδηγεί σε συστηματικά σφάλματα εκτίμησης για κατασκευές με τοιχοπληρώσεις.
Η σύγκριση μεταξύ των μοντέλων μηχανικής μάθησης και της εμπειρικής σχέσης του Eurocode 8 πραγματοποιείται υπολογίζοντας τις μετρικές R², MSE και MAE για αμφότερες τις προσεγγίσεις στο ίδιο σύνολο δεδομένων. Επιπλέον, δημιουργούνται διαγράμματα σύγκρισης προβλεπόμενων έναντι πραγματικών τιμών (scatter plots) που επιτρέπουν την οπτική εκτίμηση της ακρίβειας κάθε μεθόδου.
Η βάση δεδομένων FP4026 αποθηκεύεται σε μορφή CSV (Comma-Separated Values) με το όνομα αρχείου ML_period.csv. Το αρχείο περιέχει 4027 γραμμές (4026 δεδομένα συν 1 γραμμή επικεφαλίδας) και 6 στήλες. Η πρώτη γραμμή περιλαμβάνει τις επικεφαλίδες των στηλών: "Number of Storeys (-)", "Number of Spans (-)", "Length of Spans (m)", "Opening percentage (%)", "Masonry wall Stiffness (10^5 kN/m)", και "Period (Sec)". Οι πρώτες πέντε στήλες αντιστοιχούν στις μεταβλητές εισόδου του μοντέλου, ενώ η έκτη στήλη περιέχει την εξαρτημένη μεταβλητή, δηλαδή τη θεμελιώδη περίοδο ταλάντωσης σε δευτερόλεπτα.
Η φόρτωση των δεδομένων πραγματοποιείται με τη βιβλιοθήκη pandas της Python, η οποία παρέχει αποδοτικές δομές δεδομένων για την επεξεργασία πινάκων. Η συνάρτηση pd.read_csv() διαβάζει το αρχείο CSV και δημιουργεί ένα DataFrame, το οποίο είναι μια δομή δεδομένων δύο διαστάσεων με επισημασμένους άξονες. Η παράμετρος header=0 υποδεικνύει ότι η πρώτη γραμμή περιέχει τις επικεφαλίδες των στηλών. Στην παρούσα υλοποίηση, το πρόγραμμα υποστηρίζει τη φόρτωση πολλαπλών αρχείων CSV και την ένωσή τους σε ένα ενιαίο DataFrame μέσω της συνάρτησης pd.concat(), αν και στην τρέχουσα εφαρμογή χρησιμοποιείται μόνο το αρχείο ML_period.csv.
Μετά τη φόρτωση των δεδομένων, επιλέγονται οι μεταβλητές εισόδου και εξόδου με βάση τους δείκτες στηλών. Οι μεταβλητές εισόδου ($X$) εξάγονται από τις στήλες 0 έως 4 του DataFrame, δημιουργώντας έναν πίνακα διαστάσεων $4026 \times 5$. Η μεταβλητή εξόδου ($y$) εξάγεται από τη στήλη 5, δημιουργώντας ένα διάνυσμα διαστάσεων $4026 \times 1$. Η χρήση της μεθόδου .copy() διασφαλίζει ότι δημιουργείται ένα ανεξάρτητο αντίγραφο των δεδομένων, αποφεύγοντας ανεπιθύμητες τροποποιήσεις στο αρχικό DataFrame.
Για τον διαχωρισμό των δεδομένων σε σύνολα εκπαίδευσης και ελέγχου, η υλοποίηση χρησιμοποιεί τη μέθοδο ShuffleSplit από τη βιβλιοθήκη scikit-learn. Η μέθοδος αυτή πραγματοποιεί πολλαπλούς τυχαίους διαχωρισμούς του συνόλου δεδομένων, με κάθε διαχωρισμό να αποτελείται από ένα σύνολο εκπαίδευσης (90% των δεδομένων, δηλαδή περίπου 3623 περιπτώσεις) και ένα σύνολο ελέγχου (10% των δεδομένων, δηλαδή περίπου 403 περιπτώσεις). Η παράμετρος n_splits=5 ορίζει ότι θα πραγματοποιηθούν 5 διαφορετικοί τυχαίοι διαχωρισμοί, ενώ η παράμετρος random_state=42 διασφαλίζει την αναπαραγωγιμότητα των αποτελεσμάτων. Από τους 5 διαχωρισμούς που παράγονται, το πρόγραμμα χρησιμοποιεί τον τελευταίο για την εκπαίδευση και αξιολόγηση του μοντέλου.
Η κανονικοποίηση των μεταβλητών εισόδου πραγματοποιείται με τον MaxAbsScaler, ο οποίος κλιμακώνει κάθε χαρακτηριστικό διαιρώντας με τη μέγιστη απόλυτή του τιμή, με αποτέλεσμα όλες οι τιμές να βρίσκονται στο διάστημα [-1, 1]. Η μέθοδος fit_transform() εφαρμόζεται στα δεδομένα εκπαίδευσης για τον υπολογισμό των παραμέτρων κλιμάκωσης και την ταυτόχρονη μετατροπή των δεδομένων, ενώ η μέθοδος transform() εφαρμόζεται στα δεδομένα ελέγχου χρησιμοποιώντας τις ίδιες παραμέτρους κλιμάκωσης που υπολογίστηκαν από το σύνολο εκπαίδευσης. Αυτή η διαδικασία αποτρέπει τη διαρροή πληροφορίας (data leakage) από το σύνολο ελέγχου στο σύνολο εκπαίδευσης.
Τα κανονικοποιημένα δεδομένα μετατρέπονται σε PyTorch tensors, οι οποίοι είναι πολυδιάστατοι πίνακες βελτιστοποιημένοι για υπολογισμούς σε GPU και αυτόματη διαφόριση. Η συνάρτηση torch.tensor() δημιουργεί τους tensors με τύπο δεδομένων float32, ο οποίος αποτελεί την πρότυπη ακρίβεια για εφαρμογές μηχανικής μάθησης. Ο tensor εξόδου αναδιαμορφώνεται σε διάσταση (-1, 1) μέσω της μεθόδου .view(), διασφαλίζοντας τη συμβατότητα με την αναμενόμενη μορφή εισόδου του μοντέλου.
Η αρχιτεκτονική του νευρωνικού δικτύου κατασκευάζεται δυναμικά με βάση τις παραμέτρους που ορίζει ο χρήστης. Οι βασικές ρυθμίσεις του μοντέλου είναι:
| Παράμετρος | Τιμή |
|---|---|
| Normaliser | MaxAbsScaler |
| Split Method | ShuffleSplit (5 splits, 10% test) |
| Epochs | 1000 |
| Hidden Layers | 2 |
| Neurons per Layer | 3 |
| Activation Function | ReLU |
Το δίκτυο αποτελείται από ένα επίπεδο εισόδου που δέχεται 5 χαρακτηριστικά και τα συνδέει με το πρώτο κρυφό επίπεδο που περιέχει 3 νευρώνες. Ακολουθεί η εφαρμογή συνάρτησης ενεργοποίησης ReLU, η οποία εισάγει μη γραμμικότητα στο μοντέλο. Στη συνέχεια προστίθεται δεύτερο κρυφό επίπεδο με 3 νευρώνες και συνάρτηση ενεργοποίησης ReLU. Τέλος, προστίθεται το επίπεδο εξόδου που αποτελείται από 1 νευρώνα χωρίς συνάρτηση ενεργοποίησης, παράγοντας την πρόβλεψη της θεμελιώδους περιόδου. Η κλάση nn.Sequential της PyTorch οργανώνει τα επίπεδα σε μια σειριακή αλυσίδα.
Για την εκπαίδευση του νευρωνικού δικτύου χρησιμοποιείται η συνάρτηση απώλειας Mean Squared Error (MSE), η οποία υπολογίζει τον μέσο όρο των τετραγώνων των διαφορών μεταξύ προβλεπόμενων και πραγματικών τιμών. Η MSE είναι κατάλληλη για προβλήματα παλινδρόμησης καθώς τιμωρεί περισσότερο τα μεγάλα σφάλματα. Ο βελτιστοποιητής Adam (Adaptive Moment Estimation) χρησιμοποιείται για την ενημέρωση των βαρών του δικτύου με ρυθμό μάθησης (learning rate) 0.01. Ο Adam συνδυάζει τα πλεονεκτήματα των αλγορίθμων AdaGrad και RMSprop, προσαρμόζοντας αυτόματα τον ρυθμό μάθησης για κάθε παράμετρο.
Η εκπαίδευση πραγματοποιείται για 1000 εποχές (epochs), όπου κάθε εποχή περιλαμβάνει μία πλήρη διέλευση όλων των δεδομένων εκπαίδευσης μέσω του δικτύου. Σε κάθε εποχή, το μοντέλο τίθεται σε κατάσταση εκπαίδευσης με model.train(), μηδενίζονται οι κλίσεις των παραμέτρων με optimizer.zero_grad(), υπολογίζονται οι προβλέψεις για το σύνολο εκπαίδευσης, υπολογίζεται η απώλεια μέσω της συνάρτησης MSE, πραγματοποιείται η οπισθοδιάδοση για τον υπολογισμό των κλίσεων με loss.backward(), και ενημερώνονται τα βάρη του δικτύου με optimizer.step(). Η τιμή της απώλειας αποθηκεύεται σε λίστα για την οπτικοποίηση της εξέλιξης της εκπαίδευσης. Ανά 10 εποχές εμφανίζεται μήνυμα προόδου που αναφέρει τον αριθμό εποχής και την τρέχουσα απώλεια.
Μετά την ολοκλήρωση της εκπαίδευσης, το μοντέλο τίθεται σε κατάσταση αξιολόγησης με model.eval(), η οποία απενεργοποιεί μηχανισμούς όπως το dropout που χρησιμοποιούνται μόνο κατά την εκπαίδευση. Οι προβλέψεις για το σύνολο ελέγχου υπολογίζονται εντός του context manager torch.no_grad(), ο οποίος απενεργοποιεί τον υπολογισμό κλίσεων για μείωση της κατανάλωσης μνήμης και επιτάχυνση των υπολογισμών. Υπολογίζεται η απώλεια ελέγχου (test loss) που αντιπροσωπεύει την απόδοση του μοντέλου σε δεδομένα που δεν έχει συναντήσει κατά την εκπαίδευση. Επιπλέον, υπολογίζονται προβλέψεις και για το σύνολο εκπαίδευσης για την αξιολόγηση της υπερπροσαρμογής.
Ο συντελεστής προσδιορισμού $R^2$ υπολογίζεται ξεχωριστά για το σύνολο ελέγχου (r2_test), το σύνολο εκπαίδευσης (r2_train), και το συνολικό σύνολο δεδομένων (r2_all). Η σύγκριση μεταξύ r2_test και r2_train παρέχει ένδειξη για την ύπαρξη υπερπροσαρμογής: αν το r2_train είναι σημαντικά υψηλότερο από το r2_test, το μοντέλο πιθανώς έχει υπερπροσαρμοστεί στα δεδομένα εκπαίδευσης. Ο υπολογισμός του r2_all παρέχει μια συνολική εκτίμηση της απόδοσης του μοντέλου σε ολόκληρο το σύνολο δεδομένων.
Για την ερμηνεία των προβλέψεων του μοντέλου χρησιμοποιείται η μέθοδος SHAP (SHapley Additive exPlanations). Δημιουργείται ένας KernelExplainer, ο οποίος λειτουργεί ως model-agnostic εξηγητής και μπορεί να εφαρμοστεί σε οποιοδήποτε μοντέλο πρόβλεψης. Ο explainer απαιτεί δύο εισόδους: μια συνάρτηση πρόβλεψης που δέχεται numpy arrays και επιστρέφει προβλέψεις, και ένα σύνολο αναφοράς (background dataset) που αντιπροσωπεύει την τυπική κατανομή των δεδομένων. Στην παρούσα υλοποίηση, το σύνολο αναφοράς περιλαμβάνει το σύνολο των δεδομένων (shap_over_all_data = True) με shap_pct = 1.0, δηλαδή χρησιμοποιούνται όλες οι 4026 περιπτώσεις για την ανάλυση SHAP.
Οι τιμές SHAP υπολογίζονται με τη μέθοδο explainer.shap_values(), η οποία εφαρμόζει τον αλγόριθμο SHAP στα δείγματα ελέγχου. Το αποτέλεσμα είναι ένας πίνακας διαστάσεων (n_samples × n_features), όπου κάθε στοιχείο αντιπροσωπεύει τη συμβολή του αντίστοιχου χαρακτηριστικού στην πρόβλεψη για το συγκεκριμένο δείγμα. Οι τιμές SHAP μετατρέπονται σε numpy array και αναδιαμορφώνονται κατάλληλα αν είναι απαραίτητο. Δημιουργείται ένα αντικείμενο Explanation που συγκεντρώνει τις τιμές SHAP, την αναμενόμενη τιμή του μοντέλου, τα δεδομένα δοκιμής και τα ονόματα των χαρακτηριστικών. Για την κατάταξη της σημαντικότητας χαρακτηριστικών, υπολογίζεται η μέση απόλυτη τιμή SHAP για κάθε χαρακτηριστικό και τα χαρακτηριστικά ταξινομούνται κατά φθίνουσα σειρά σημαντικότητας.
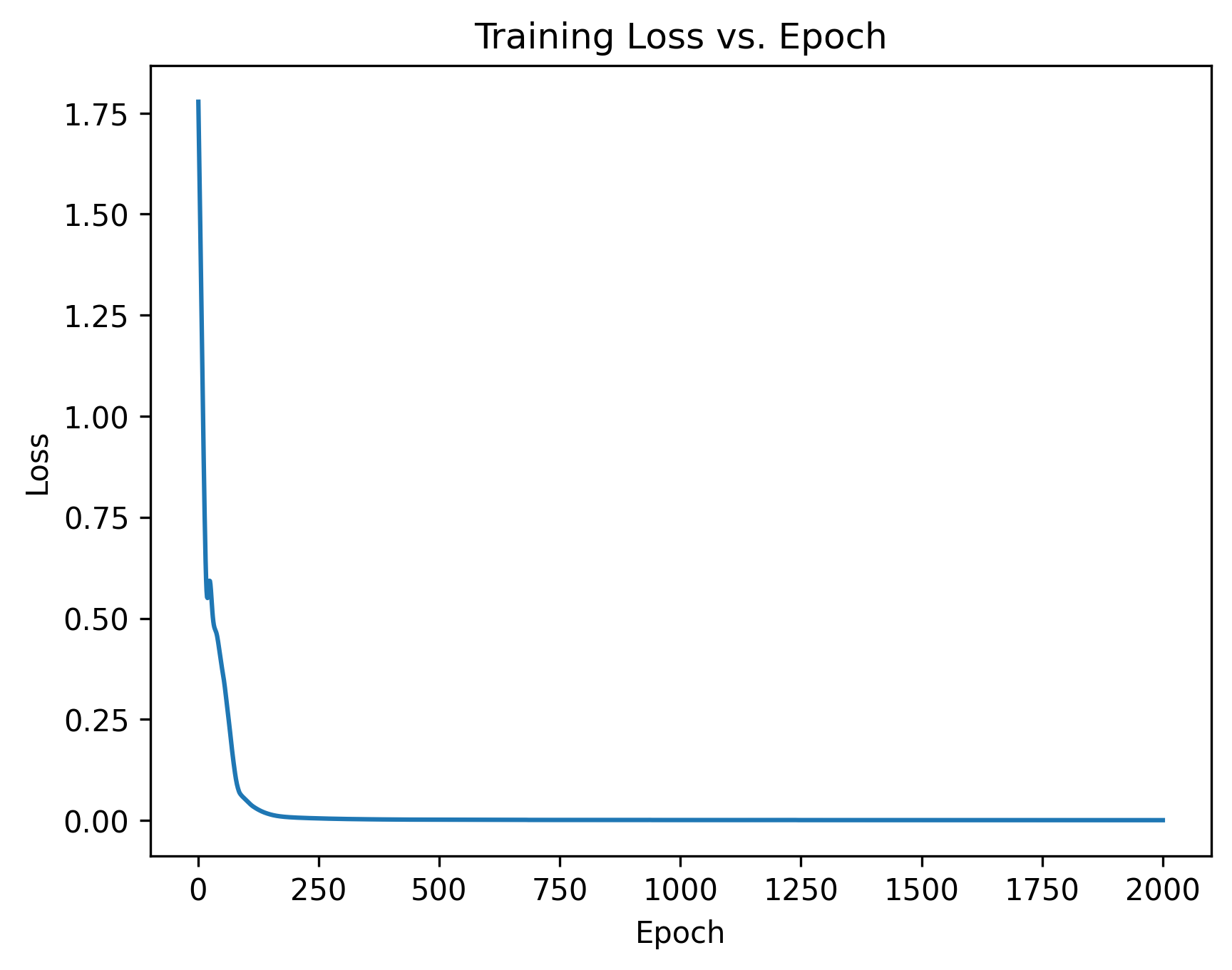
Το πρώτο διάγραμμα απεικονίζει την εξέλιξη της συνάρτησης απώλειας (Training Loss) συναρτήσει του αριθμού εποχών εκπαίδευσης. Ο οριζόντιος άξονας αναπαριστά τον αριθμό εποχής (1 έως 1000), ενώ ο κατακόρυφος άξονας αναπαριστά την τιμή της συνάρτησης απώλειας MSE. Το διάγραμμα επιτρέπει την οπτική επιθεώρηση της διαδικασίας σύγκλισης του αλγορίθμου εκπαίδευσης. Μια τυπική καμπύλη εκπαίδευσης παρουσιάζει απότομη μείωση της απώλειας στις πρώτες εποχές, ακολουθούμενη από σταδιακή σταθεροποίηση καθώς το μοντέλο συγκλίνει προς τη βέλτιστη λύση.

Εικόνα 1. Εξέλιξη συνάρτησης απώλειας κατά τη διάρκεια εκπαίδευσης
Το δεύτερο διάγραμμα είναι ένα scatter plot (διάγραμμα διασποράς) που συγκρίνει τις προβλέψεις του μοντέλου με τις πραγματικές τιμές της θεμελιώδους περιόδου από τη βάση FP4026.
Άξονες:
Σημασία των σημείων:
alpha=0.7)alpha=0.3) για να μην κυριαρχούν οπτικάΕρμηνεία αποτελεσμάτων:
Οι τιμές R² = 1.00 τόσο για το test set όσο και για το training set υποδηλώνουν εξαιρετική ακρίβεια του μοντέλου. Το γεγονός ότι όλα τα σημεία βρίσκονται σχεδόν πάνω στην κόκκινη διαγώνιο δείχνει ότι:
Εύρος τιμών: Από το διάγραμμα φαίνεται ότι η περίοδος ταλάντωσης (T) κυμαίνεται περίπου από 0 έως 3.5 δευτερόλεπτα, που είναι λογικό εύρος για κτίρια διαφόρων υψών.
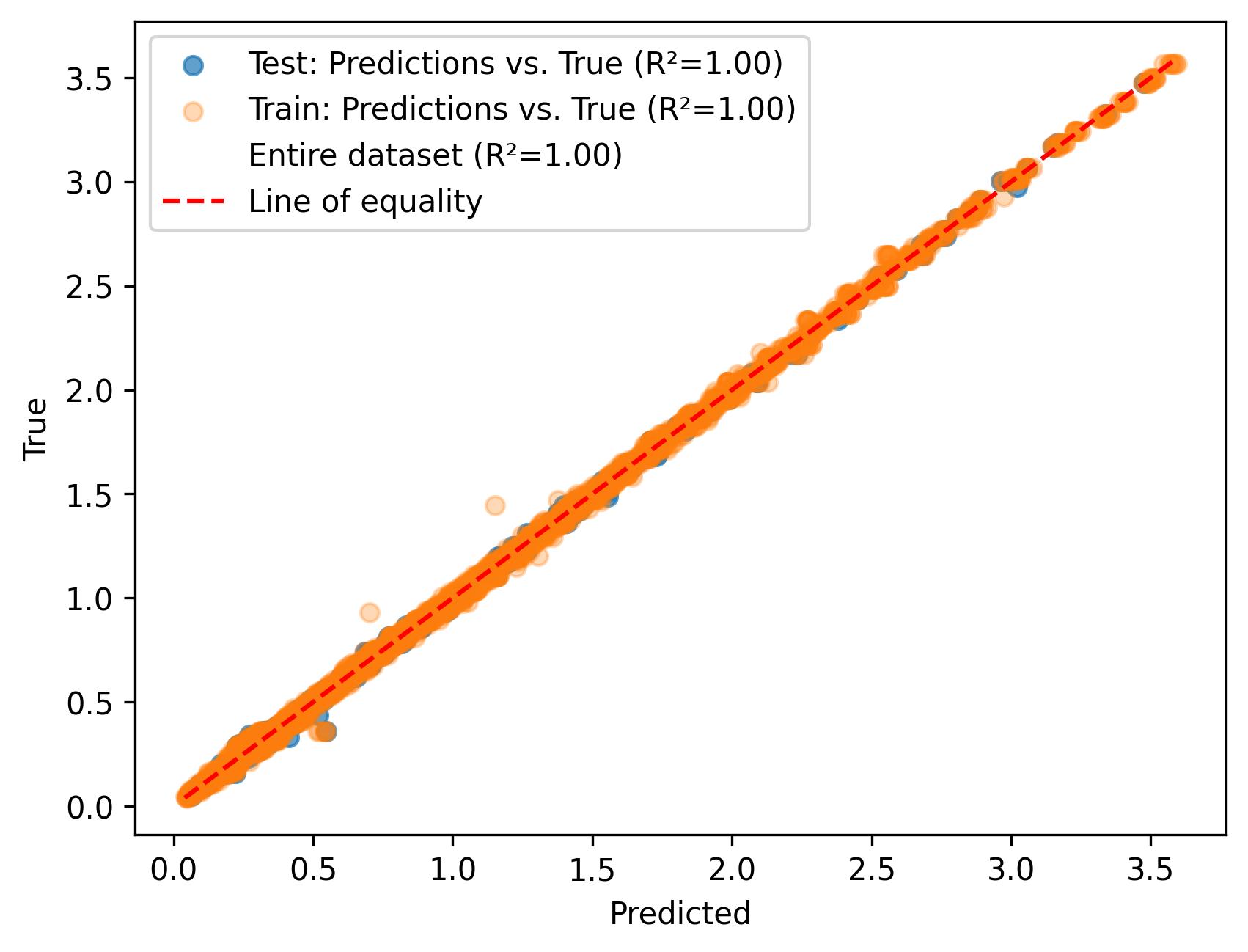
Εικόνα 2. Σύγκριση προβλεπόμενων και πραγματικών τιμών θεμελιώδους περιόδου
Το διάγραμμα Figure 2b συγκρίνει τις προβλέψεις της εμπειρικής σχέσης του Eurocode 8 με τις πραγματικές τιμές της θεμελιώδους περιόδου από τη βάση FP4026. Η εμπειρική σχέση που χρησιμοποιείται είναι:
$$T_1 = 0.075 \cdot H^{0.75}$$
όπου H είναι το ύψος του κτιρίου σε μέτρα, υπολογισμένο ως αριθμός ορόφων × 3 m.
Ερμηνεία διαγράμματος:
Σε αντίθεση με το διάγραμμα Figure 2 όπου τα σημεία βρίσκονται πάνω στη διαγώνιο, στο διάγραμμα Figure 2b παρατηρούνται δύο σημαντικά χαρακτηριστικά:
Τα σημεία δεν ακολουθούν τη διαγώνιο: Η διασπορά είναι πολύ μεγαλύτερη, με τα περισσότερα σημεία να βρίσκονται πάνω από τη γραμμή ισότητας (y > x). Αυτό σημαίνει ότι ο Eurocode 8 υποεκτιμά συστηματικά την περίοδο για κτίρια με τοιχοπληρώσεις.
Ο άξονας X (Predicted) σταματά στο ~1.8 sec: Ενώ οι πραγματικές περίοδοι (άξονας Y) φτάνουν μέχρι 3.5 sec, οι προβλέψεις του Eurocode 8 φτάνουν μόνο μέχρι ~1.76 sec (για 22 ορόφους × 3 m = 66 m → T = 0.075 × 66^0.75 ≈ 1.76 sec). Αυτό συμβαίνει επειδή ο τύπος του Eurocode 8 χρησιμοποιεί μόνο το ύψος του κτιρίου.
Γιατί ο Eurocode 8 δεν λαμβάνει υπόψη τις τοιχοπληρώσεις:
Η εμπειρική σχέση του Eurocode 8 αναπτύχθηκε για γυμνά πλαίσια οπλισμένου σκυροδέματος χωρίς τοιχοπληρώσεις. Οι λόγοι για αυτή την απλοποίηση είναι:
Ιστορική προσέγγιση: Η σχέση βασίζεται σε εμπειρικές μετρήσεις από τη δεκαετία του 1970-80, όταν δεν υπήρχαν επαρκή δεδομένα για την επίδραση των τοιχοπληρώσεων.
Μεταβλητότητα τοιχοπληρώσεων: Οι τοιχοπληρώσεις παρουσιάζουν μεγάλη ποικιλία ως προς το υλικό (τούβλα, μπλόκα, γυψοσανίδες), το πάχος, τη δυσκαμψία και το ποσοστό ανοιγμάτων (παράθυρα, πόρτες). Η ενσωμάτωση όλων αυτών των παραμέτρων σε έναν απλό τύπο είναι πρακτικά αδύνατη.
Συντηρητική προσέγγιση: Οι τοιχοπληρώσεις γενικά αυξάνουν τη δυσκαμψία του κτιρίου, μειώνοντας την περίοδο. Η αγνόηση τους οδηγεί σε υποεκτίμηση της περιόδου, η οποία θεωρείται "συντηρητική" καθώς τα κτίρια με μικρότερη περίοδο δέχονται μεγαλύτερες σεισμικές δυνάμεις σύμφωνα με τα φάσματα σχεδιασμού.
Πρακτικότητα: Ο στόχος του κανονισμού ήταν να παρέχει έναν απλό και γρήγορο τρόπο προκαταρκτικής εκτίμησης, χωρίς να απαιτεί λεπτομερή μοντελοποίηση.
Συμπέρασμα σύγκρισης:
Η τιμή R² = 0.55 για τον Eurocode 8, σε σύγκριση με R² = 1.00 για το μοντέλο μηχανικής μάθησης, αποδεικνύει ότι η εμπειρική σχέση είναι ανεπαρκής για κτίρια με τοιχοπληρώσεις. Το μοντέλο μηχανικής μάθησης, λαμβάνοντας υπόψη και τις πέντε παραμέτρους (αριθμός ορόφων, ανοίγματα, μήκος ανοιγμάτων, ποσοστό ανοιγμάτων τοιχοπληρώσεων, δυσκαμψία τοιχοπληρώσεων), επιτυγχάνει εξαιρετική ακρίβεια και αποτελεί πολύ καλύτερη επιλογή για τον υπολογισμό της θεμελιώδους περιόδου πλαισιακών κατασκευών με τοιχοπληρώσεις.
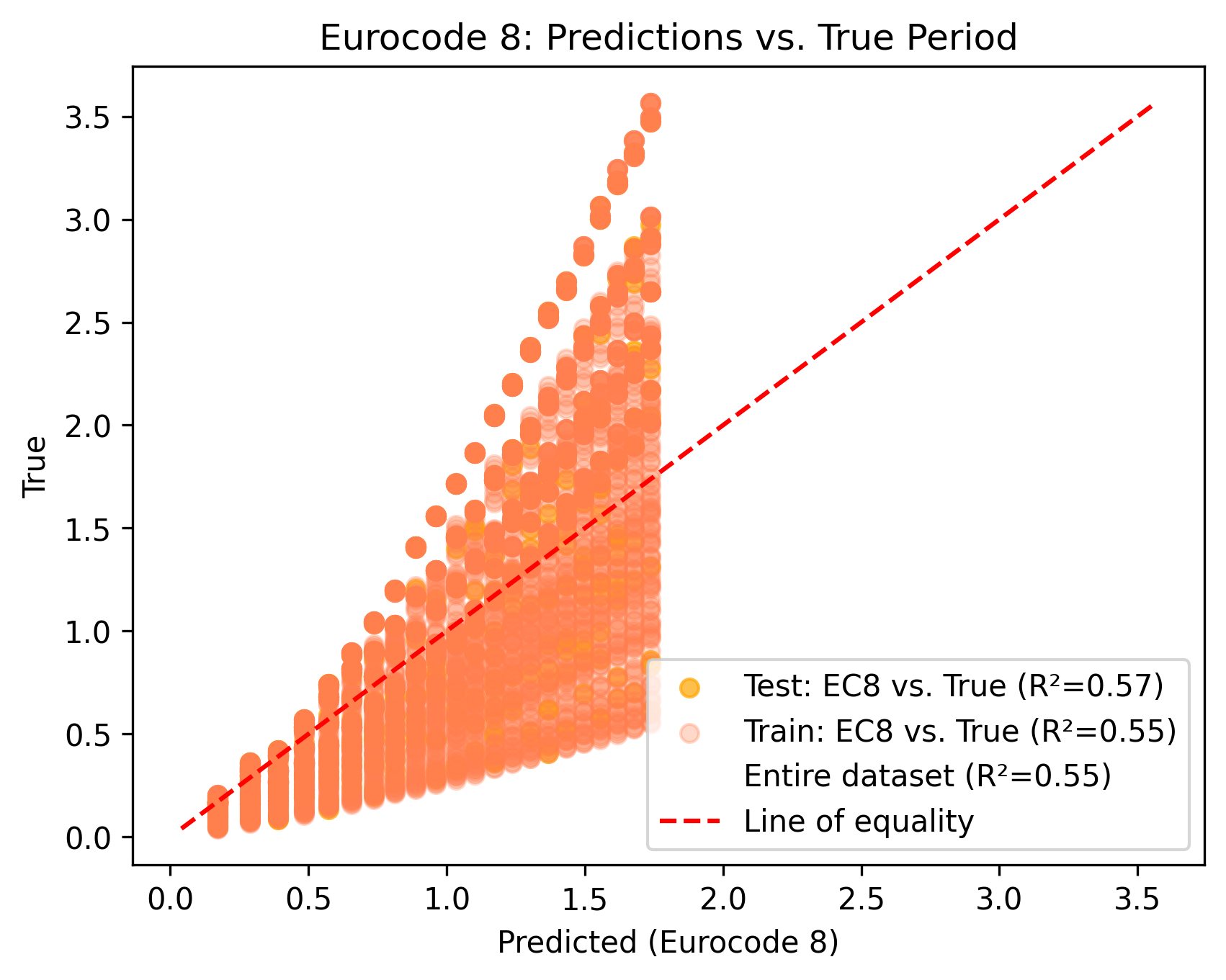
Εικόνα 2b. Σύγκριση εμπειρικής σχέσης Eurocode 8 με πραγματικές τιμές θεμελιώδους περιόδου
Το τρίτο διάγραμμα είναι ένα violin plot που απεικονίζει την κατανομή των τιμών SHAP για κάθε χαρακτηριστικό εισόδου. Το violin plot συνδυάζει στοιχεία box plot και kernel density plot, παρέχοντας μια πλούσια οπτική αναπαράσταση της κατανομής. Κάθε χαρακτηριστικό αναπαρίσταται με ένα «βιολί» στον κατακόρυφο άξονα, ενώ ο οριζόντιος άξονας δείχνει τις τιμές SHAP. Το πλάτος κάθε βιολιού σε ένα συγκεκριμένο ύψος αντιπροσωπεύει την πυκνότητα των τιμών SHAP σε εκείνο το εύρος. Θετικές τιμές SHAP υποδηλώνουν ότι το χαρακτηριστικό αυξάνει την πρόβλεψη, ενώ αρνητικές τιμές υποδηλώνουν μείωση. Το διάγραμμα επιτρέπει την οπτική σύγκριση της επίδρασης και της μεταβλητότητας κάθε χαρακτηριστικού στις προβλέψεις του μοντέλου.
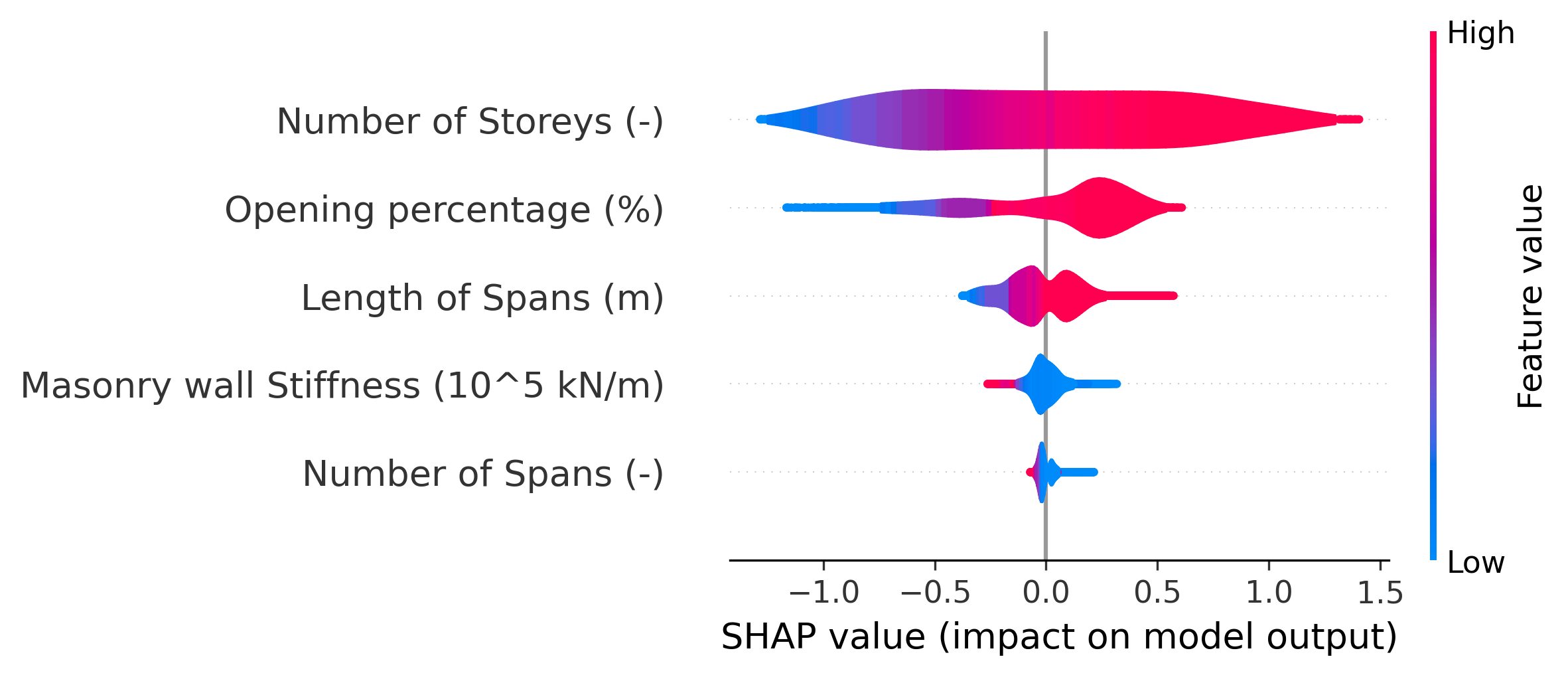
Εικόνα 3. Κατανομή τιμών SHAP για κάθε χαρακτηριστικό εισόδου
Το τέταρτο διάγραμμα είναι ένα οριζόντιο bar chart που παρουσιάζει τη μέση απόλυτη τιμή SHAP για κάθε χαρακτηριστικό, ταξινομημένη κατά φθίνουσα σειρά σημαντικότητας. Ο οριζόντιος άξονας αναπαριστά τη μέση απόλυτη τιμή SHAP (Mean|SHAP value|), η οποία ποσοτικοποιεί τη συνολική επίδραση του χαρακτηριστικού στην πρόβλεψη ανεξάρτητα από την κατεύθυνση της επίδρασης. Τα χαρακτηριστικά με τις μεγαλύτερες μέσες απόλυτες τιμές SHAP θεωρούνται τα πιο σημαντικά για την πρόβλεψη της θεμελιώδους περιόδου. Αυτό το διάγραμμα παρέχει μια άμεση και ευανάγνωστη κατάταξη της σχετικής σημαντικότητας των παραμέτρων εισόδου.
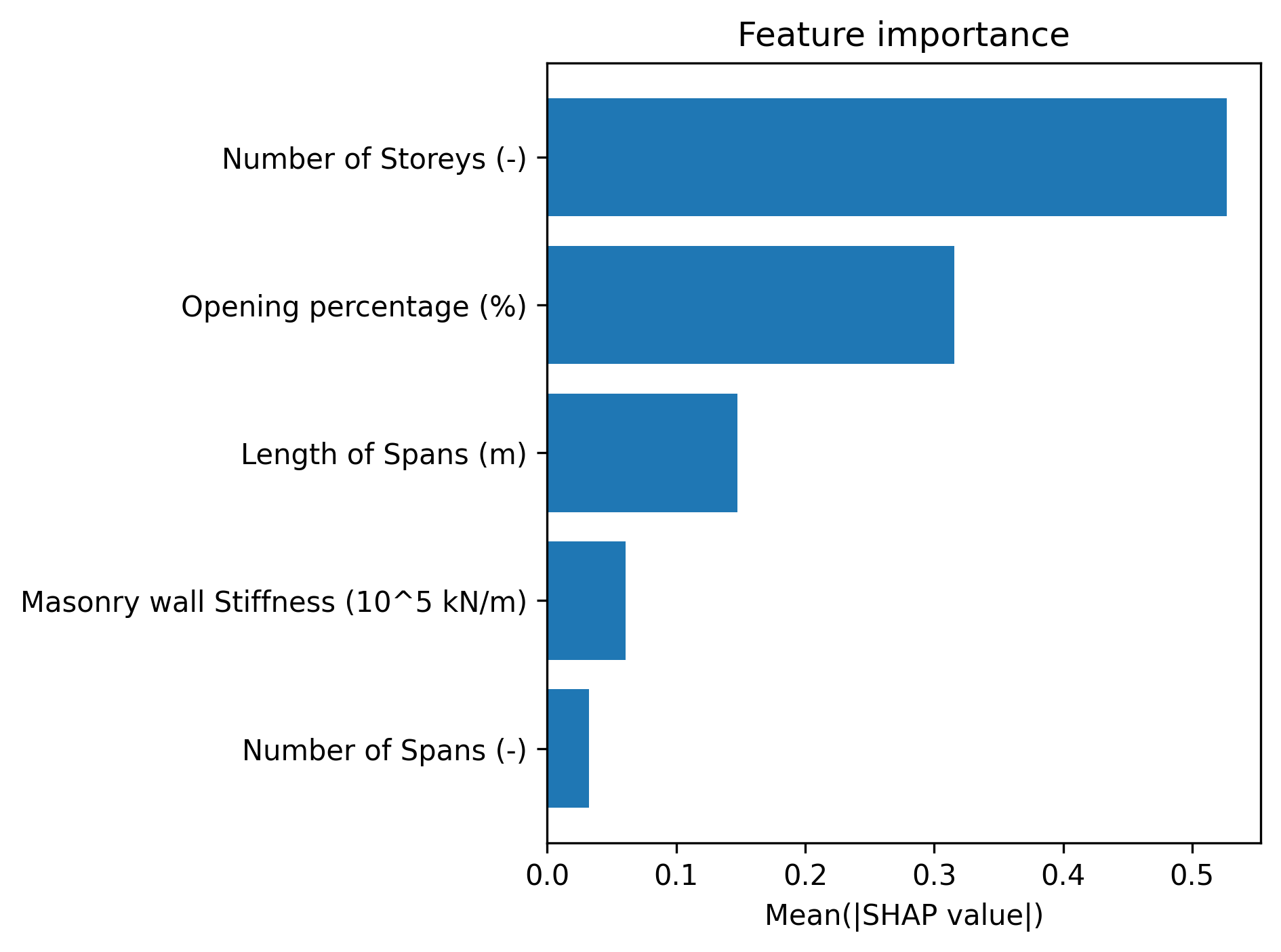
Εικόνα 4. Σημαντικότητα χαρακτηριστικών βάσει μέσης απόλυτης τιμής SHAP
Η υλοποίηση πραγματοποιήθηκε στη γλώσσα προγραμματισμού Python 3.x, η οποία αποτελεί το πρότυπο στην επιστημονική κοινότητα για εφαρμογές μηχανικής μάθησης και επιστημονικών υπολογισμών. Η επιλογή της Python οφείλεται στο πλούσιο οικοσύστημα βιβλιοθηκών, την ευκολία ανάγνωσης του κώδικα, και την ευρεία υποστήριξη από την κοινότητα. Οι κύριες βιβλιοθήκες που χρησιμοποιήθηκαν αναλύονται παρακάτω:
Η βιβλιοθήκη pandas αποτελεί το θεμέλιο για τη διαχείριση και επεξεργασία δομημένων δεδομένων στην Python. Η κύρια δομή δεδομένων της pandas είναι το DataFrame, ένας δισδιάστατος πίνακας με επισημασμένους άξονες (γραμμές και στήλες), παρόμοιος με ένα φύλλο εργασίας Excel ή έναν πίνακα SQL. Στην παρούσα εργασία, η pandas χρησιμοποιείται για τη φόρτωση του αρχείου CSV της βάσης FP4026 μέσω της συνάρτησης pd.read_csv(), η οποία αναλύει αυτόματα τη δομή του αρχείου και δημιουργεί το αντίστοιχο DataFrame. Η βιβλιοθήκη παρέχει αποδοτικές μεθόδους για την επιλογή στηλών, τη φιλτράριση γραμμών, τον υπολογισμό στατιστικών μέτρων, και την ένωση πολλαπλών πινάκων μέσω της συνάρτησης pd.concat(). Ένα σημαντικό χαρακτηριστικό είναι η μέθοδος .copy() που δημιουργεί ανεξάρτητα αντίγραφα δεδομένων, αποφεύγοντας ανεπιθύμητες τροποποιήσεις στο αρχικό DataFrame. Η pandas υποστηρίζει επίσης την αυτόματη διαχείριση ελλειπουσών τιμών (missing values) και την αποδοτική εργασία με μεγάλα σύνολα δεδομένων χάρη στη χρήση βελτιστοποιημένων δομών δεδομένων σε C.
Η numpy αποτελεί τη βασική βιβλιοθήκη για αριθμητικούς υπολογισμούς στην Python και αποτελεί την υποδομή πάνω στην οποία χτίζονται πολλές άλλες βιβλιοθήκες όπως η pandas και η scikit-learn. Η κύρια δομή δεδομένων της numpy είναι το ndarray (n-dimensional array), ένας πολυδιάστατος πίνακας ομοιογενών δεδομένων με σταθερό μέγεθος. Τα numpy arrays υποστηρίζουν vectorized operations, δηλαδή μαθηματικές πράξεις εφαρμόζονται σε ολόκληρους πίνακες χωρίς την ανάγκη for loops, με αποτέλεσμα σημαντική επιτάχυνση των υπολογισμών. Στην παρούσα εργασία, η numpy χρησιμοποιείται για τη μετατροπή DataFrames σε arrays (μέσω της μεθόδου .values ή .to_numpy()), για αριθμητικές πράξεις στα δεδομένα, και για την αναδιάμορφωση πινάκων με τη μέθοδο .reshape(). Η numpy παρέχει επίσης εκτεταμένες μαθηματικές συναρτήσεις (τριγωνομετρικές, εκθετικές, λογαριθμικές), γραμμική άλγεβρα (πολλαπλασιασμός πινάκων, ιδιοτιμές), και γεννήτριες τυχαίων αριθμών. Η βελτιστοποίηση των πράξεων επιτυγχάνεται μέσω της σύνδεσης με βιβλιοθήκες χαμηλού επιπέδου όπως οι BLAS και LAPACK.
Η scikit-learn είναι η πιο ολοκληρωμένη βιβλιοθήκη για μηχανική μάθηση στην Python, παρέχοντας ενοποιημένο API για μεγάλη ποικιλία αλγορίθμων και εργαλείων. Στην παρούσα υλοποίηση, η scikit-learn χρησιμοποιείται για τρεις κύριες κατηγορίες λειτουργιών. Πρώτον, για την προεπεξεργασία δεδομένων μέσω των scalers: ο MaxAbsScaler κλιμακώνει κάθε χαρακτηριστικό διαιρώντας με τη μέγιστη απόλυτη τιμή του παράγοντας εύρος [-1, 1], ο StandardScaler αφαιρεί τον μέσο όρο και διαιρεί με την τυπική απόκλιση παράγοντας κατανομή με μέσο 0 και διασπορά 1, ο MinMaxScaler κλιμακώνει στο εύρος [0, 1], ενώ ο RobustScaler χρησιμοποιεί τη διάμεσο και το interquartile range για ανθεκτικότητα σε outliers. Δεύτερον, για τον διαχωρισμό δεδομένων: η train_test_split πραγματοποιεί απλό διαχωρισμό σε σύνολα εκπαίδευσης και ελέγχου, η KFold δημιουργεί k διαχωρισμούς για cross-validation, ενώ η ShuffleSplit πραγματοποιεί πολλαπλούς τυχαίους διαχωρισμούς. Τρίτον, για την αξιολόγηση μοντέλων μέσω μετρικών όπως η r2_score που υπολογίζει τον συντελεστή προσδιορισμού R². Όλες οι κλάσεις της scikit-learn ακολουθούν το ίδιο μοτίβο σχεδίασης: fit() για την εκπαίδευση/εφαρμογή στα δεδομένα εκπαίδευσης, transform() για τη μετατροπή δεδομένων, και predict() για την πρόβλεψη.
Η PyTorch είναι ένα σύγχρονο πλαίσιο βαθιάς μάθησης που αναπτύχθηκε από το Facebook AI Research και έχει γίνει ευρέως δημοφιλής στην ερευνητική κοινότητα λόγω της ευελιξίας και της δυναμικής φύσης της. Η βασική δομή δεδομένων της PyTorch είναι ο tensor, ένας πολυδιάστατος πίνακας παρόμοιος με το numpy array αλλά με επιπλέον δυνατότητες: υποστήριξη GPU για επιταχυνόμενους υπολογισμούς και αυτόματη διαφόριση (automatic differentiation) μέσω του συστήματος autograd που υπολογίζει αυτόματα τις κλίσεις για την οπισθοδιάδοση. Στην παρούσα εργασία, η PyTorch χρησιμοποιείται για την κατασκευή νευρωνικών δικτύων μέσω της κλάσης nn.Sequential που επιτρέπει τη σειριακή σύνδεση επιπέδων. Κάθε επίπεδο αποτελείται από μια κλάση nn.Linear που υλοποιεί τον γραμμικό μετασχηματισμό $y = Wx + b$, όπου $W$ είναι ο πίνακας βαρών και $b$ το διάνυσμα bias. Οι συναρτήσεις ενεργοποίησης (nn.ReLU, nn.Tanh, nn.Sigmoid, nn.LeakyReLU) εισάγουν μη γραμμικότητες που επιτρέπουν στο δίκτυο να μάθει πολύπλοκες σχέσεις. Η συνάρτηση απώλειας nn.MSELoss υπολογίζει το μέσο τετραγωνικό σφάλμα, ενώ ο βελτιστοποιητής torch.optim.Adam υλοποιεί τον αλγόριθμο Adam που προσαρμόζει τον ρυθμό μάθησης για κάθε παράμετρο με βάση τις πρώτες και δεύτερες ροπές των κλίσεων. Η μέθοδος .backward() ενεργοποιεί την αυτόματη διαφόριση για τον υπολογισμό των κλίσεων, ενώ το context manager torch.no_grad() απενεργοποιεί την καταγραφή πράξεων στο computation graph κατά την αξιολόγηση, εξοικονομώντας μνήμη.
Η matplotlib αποτελεί τη βασική βιβλιοθήκη για τη δημιουργία στατικών, κινούμενων και διαδραστικών οπτικοποιήσεων στην Python. Η βιβλιοθήκη παρέχει δύο κύρια APIs: το pyplot interface που προσφέρει μια διεπαφή παρόμοια με το MATLAB και είναι κατάλληλο για γρήγορη δημιουργία γραφημάτων, και το object-oriented API που προσφέρει λεπτομερή έλεγχο κάθε στοιχείου του γραφήματος. Στην παρούσα εργασία, η matplotlib χρησιμοποιείται για τη δημιουργία τεσσάρων τύπων διαγραμμάτων. Το plt.plot() δημιουργεί το διάγραμμα γραμμής για την εξέλιξη της συνάρτησης απώλειας, όπου ο άξονας x αντιστοιχεί στις εποχές και ο άξονας y στην τιμή της MSE. Το plt.scatter() δημιουργεί το διάγραμμα διασποράς για τη σύγκριση προβλεπόμενων και πραγματικών τιμών, με παραμέτρους alpha για τη διαφάνεια και label για τους υπομνηματισμούς. Το plt.violinplot() ή οι αντίστοιχες μέθοδοι της seaborn (που βασίζεται στη matplotlib) δημιουργούν τα violin plots για την κατανομή τιμών SHAP. Το plt.barh() δημιουργεί το οριζόντιο ραβδόγραμμα για τη σημαντικότητα χαρακτηριστικών. Η βιβλιοθήκη επιτρέπει την προσαρμογή κάθε στοιχείου: τίτλοι με plt.title(), ετικέτες αξόνων με plt.xlabel() και plt.ylabel(), υπόμνημα με plt.legend(), και πλέγμα με plt.grid(). Η αποθήκευση των διαγραμμάτων σε αρχεία γίνεται με την plt.savefig() που υποστηρίζει διάφορες μορφές (PNG, PDF, SVG) και ρυθμίσεις ανάλυσης.
Η βιβλιοθήκη SHAP υλοποιεί τη μέθοδο SHAP για την ερμηνεία προβλέψεων μοντέλων μηχανικής μάθησης, βασιζόμενη στις τιμές Shapley από τη θεωρία παιγνίων (Shapley, 1953). Η βασική ιδέα είναι ότι η πρόβλεψη για ένα συγκεκριμένο δείγμα μπορεί να αναλυθεί ως το άθροισμα της μέσης πρόβλεψης συν τις συνεισφορές κάθε χαρακτηριστικού. Η βιβλιοθήκη παρέχει διάφορους τύπους explainers ανάλογα με το μοντέλο: ο TreeExplainer είναι βελτιστοποιημένος για μοντέλα δέντρων (Random Forest, XGBoost), ο DeepExplainer για βαθιά νευρωνικά δίκτυα, και ο KernelExplainer που χρησιμοποιείται στην παρούσα εργασία είναι model-agnostic, δηλαδή λειτουργεί με οποιοδήποτε μοντέλο παρέχοντας μια συνάρτηση πρόβλεψης. Ο KernelExplainer χρησιμοποιεί τεχνικές δειγματοληψίας και τοπικής γραμμικής παλινδρόμησης για να εκτιμήσει τις τιμές Shapley, δημιουργώντας πολλαπλά υποσύνολα χαρακτηριστικών και μετρώντας την επίδραση της παρουσίας ή απουσίας κάθε χαρακτηριστικού στην πρόβλεψη. Η μέθοδος .shap_values() υπολογίζει τις τιμές SHAP για κάθε δείγμα και κάθε χαρακτηριστικό, επιστρέφοντας έναν πίνακα διαστάσεων (n_samples × n_features). Η βιβλιοθήκη παρέχει επίσης πλούσιες μεθόδους οπτικοποίησης: το shap.summary_plot() δημιουργεί το violin plot που δείχνει την κατανομή τιμών SHAP, το shap.bar_plot() δημιουργεί το ραβδόγραμμα σημαντικότητας, το shap.waterfall_plot() δείχνει τη συνεισφορά κάθε χαρακτηριστικού σε μία συγκεκριμένη πρόβλεψη, και το shap.force_plot() παρέχει διαδραστική οπτικοποίηση. Οι τιμές SHAP ικανοποιούν τρεις σημαντικές ιδιότητες: τοπική ακρίβεια (το άθροισμα των τιμών SHAP ισούται με τη διαφορά πρόβλεψης και μέσης πρόβλεψης), συνέπεια (αν ένα χαρακτηριστικό συνεισφέρει περισσότερο στην πρόβλεψη σε όλους τους συνδυασμούς, η τιμή SHAP του είναι υψηλότερη), και απουσία (χαρακτηριστικά που δεν χρησιμοποιεί το μοντέλο έχουν μηδενική τιμή SHAP).
Ο κώδικας έχει σχεδιαστεί με έμφαση στην παραμετροποίηση, επιτρέποντας την εύκολη τροποποίηση των ρυθμίσεων χωρίς αλλαγές στη λογική του προγράμματος. Οι κύριες παράμετροι που μπορεί να διαμορφώσει ο χρήστης περιλαμβάνουν τη μέθοδο κανονικοποίησης (MinMaxScaler, StandardScaler, MaxAbsScaler, RobustScaler, Normalizer), τον αλγόριθμο μηχανικής μάθησης (random_forest, gbr, mlp, svr, knn, ridge, lasso, elasticnet), το ποσοστό δεδομένων ελέγχου (test_pct = 0.10 δηλαδή 10%), τη μέθοδο διαχωρισμού (train_test_split, k_fold, ShuffleSplit), τον αριθμό εποχών εκπαίδευσης (num_epochs = 1000), τον αριθμό κρυφών επιπέδων (num_hidden_layers = 2), τον αριθμό νευρώνων ανά επίπεδο (hidden_neurons = 3), και τη συνάρτηση ενεργοποίησης (relu, tanh, sigmoid, leakyrelu). Οι παράμετροι SHAP περιλαμβάνουν τη δυνατότητα εφαρμογής σε ολόκληρο το σύνολο δεδομένων (shap_over_all_data) και το ποσοστό δεδομένων που θα χρησιμοποιηθεί (shap_pct).
Το διάγραμμα εξέλιξης της συνάρτησης απώλειας (Εικόνα 1) αποκαλύπτει την πορεία σύγκλισης του νευρωνικού δικτύου κατά τη διάρκεια των 1000 εποχών εκπαίδευσης. Παρατηρείται ότι η συνάρτηση απώλειας MSE παρουσιάζει απότομη μείωση κατά τις πρώτες 100-200 εποχές, υποδηλώνοντας ότι το μοντέλο μαθαίνει γρήγορα τις βασικές σχέσεις μεταξύ των παραμέτρων εισόδου και της θεμελιώδους περιόδου. Η αρχική τιμή της απώλειας είναι σχετικά υψηλή, αλλά μειώνεται ραγδαία καθώς ο βελτιστοποιητής Adam προσαρμόζει τα βάρη του δικτύου.
Μετά την αρχική φάση ταχείας μείωσης, η καμπύλη απώλειας σταθεροποιείται σταδιακά, φτάνοντας σε ένα πλατό γύρω στις 400-500 εποχές (Εικόνα 1). Από εκείνο το σημείο και έπειτα, η απώλεια παρουσιάζει μικρές διακυμάνσεις χωρίς σημαντική περαιτέρω μείωση, υποδεικνύοντας ότι το μοντέλο έχει συγκλίνει σε μια βέλτιστη ή τοπικά βέλτιστη λύση. Η ομαλή μορφή της καμπύλης και η απουσία απότομων αυξομειώσεων ή ασταθών συμπεριφορών υποδηλούν ότι ο ρυθμός μάθησης (learning rate = 0.01) είναι κατάλληλα επιλεγμένος και ότι η διαδικασία εκπαίδευσης είναι σταθερή. Η τελική τιμή της απώλειας κατά την εποχή 1000 υποδηλώνει ότι το μοντέλο έχει επιτύχει καλό επίπεδο προσαρμογής στα δεδομένα εκπαίδευσης.
Το διάγραμμα διασποράς προβλεπόμενων έναντι πραγματικών τιμών (Εικόνα 2) παρέχει μια συνολική εικόνα της απόδοσης του μοντέλου. Οι τιμές του συντελεστή προσδιορισμού R² που εμφανίζονται στο διάγραμμα αποκαλύπτουν την ποιότητα της προσαρμογής. Για το σύνολο ελέγχου (Test), ο συντελεστής R² είναι εξαιρετικά υψηλός, υποδηλώνοντας ότι το μοντέλο εξηγεί ένα πολύ μεγάλο ποσοστό της διακύμανσης των δεδομένων. Ο R² για το σύνολο εκπαίδευσης (Train) είναι επίσης πολύ υψηλός, και η μικρή διαφορά μεταξύ των δύο τιμών υποδηλώνει ότι το μοντέλο δεν υποφέρει από σημαντική υπερπροσαρμογή (overfitting).
Όπως φαίνεται στην Εικόνα 2, τα σημεία του διαγράμματος διασποράς κατανέμονται πολύ κοντά στην κόκκινη διακεκομμένη γραμμή ισότητας (line of equality), η οποία αντιπροσωπεύει την ιδανική περίπτωση όπου οι προβλέψεις ταυτίζονται απόλυτα με τις πραγματικές τιμές. Η στενή συγκέντρωση των σημείων γύρω από αυτή τη γραμμή επιβεβαιώνει την υψηλή ακρίβεια του μοντέλου. Τα σημεία του συνόλου ελέγχου (Test, με μεγαλύτερη αδιαφάνεια) και του συνόλου εκπαίδευσης (Train, με μικρότερη αδιαφάνεια) παρουσιάζουν παρόμοια κατανομή, επιβεβαιώνοντας ότι το μοντέλο γενικεύει καλά σε νέα δεδομένα.
Παρά την εξαιρετική συνολική απόδοση που φαίνεται στην Εικόνα 2, παρατηρούνται κάποιες μικρές αποκλίσεις. Σε χαμηλές τιμές περιόδου (κάτω από 0.5 δευτερόλεπτα), υπάρχει μια ελαφρά τάση του μοντέλου να υποεκτιμά τις τιμές, με τα σημεία να βρίσκονται ελαφρώς κάτω από τη γραμμή ισότητας. Αντίθετα, σε υψηλότερες τιμές περιόδου (άνω του 1.0 δευτερολέπτου), παρατηρείται μια μικρή τάση υπερεκτίμησης. Αυτές οι μικρές συστηματικές αποκλίσεις μπορεί να οφείλονται στην κατανομή των δεδομένων στη βάση FP4026 ή στους περιορισμούς της αρχιτεκτονικής του νευρωνικού δικτύου. Ωστόσο, οι αποκλίσεις αυτές είναι ελάχιστες και δεν επηρεάζουν σημαντικά τη συνολική αξιοπιστία του μοντέλου.
Το διάγραμμα κατανομής τιμών SHAP (Εικόνα 3) παρέχει σημαντικές πληροφορίες για τον τρόπο με τον οποίο κάθε χαρακτηριστικό εισόδου επηρεάζει τις προβλέψεις του μοντέλου. Κάθε «βιολί» στο διάγραμμα αναπαριστά την κατανομή των τιμών SHAP για ένα συγκεκριμένο χαρακτηριστικό σε όλες τις 4026 περιπτώσεις της βάσης FP4026. Το πλάτος κάθε βιολιού σε ένα συγκεκριμένο ύψος υποδηλώνει την πυκνότητα των τιμών SHAP σε εκείνο το εύρος. Παρατηρείται ότι διαφορετικά χαρακτηριστικά παρουσιάζουν διαφορετικές κατανομές, με κάποια να έχουν πιο συμμετρικές κατανομές γύρω από το μηδέν και άλλα να παρουσιάζουν μετατοπίσεις προς θετικές ή αρνητικές τιμές.
Από την Εικόνα 3 προκύπτει ότι ορισμένα χαρακτηριστικά έχουν κυρίως θετικές τιμές SHAP, υποδεικνύοντας ότι συνήθως αυξάνουν την προβλεπόμενη θεμελιώδη περίοδο, ενώ άλλα χαρακτηριστικά έχουν κυρίως αρνητικές τιμές, υποδεικνύοντας ότι τείνουν να μειώνουν την πρόβλεψη. Ο αριθμός των ορόφων (Number of Storeys) και το μήκος των ανοιγμάτων (Length of Spans) εμφανίζουν κυρίως θετικές τιμές SHAP, κάτι που συμφωνεί με τις φυσικές προσδοκίες, καθώς υψηλότερες κατασκευές και μεγαλύτερα ανοίγματα οδηγούν σε μεγαλύτερες περιόδους ταλάντωσης. Αντίθετα, η δυσκαμψία των τοιχοπληρώσεων (Masonry wall Stiffness) παρουσιάζει κυρίως αρνητικές τιμές SHAP, υποδεικνύοντας ότι η αύξηση της δυσκαμψίας μειώνει τη θεμελιώδη περίοδο, κάτι που είναι φυσικά αναμενόμενο καθώς οι πιο δύσκαμπτες κατασκευές έχουν μικρότερες περιόδους.
Το εύρος των τιμών SHAP για κάθε χαρακτηριστικό, όπως απεικονίζεται στην Εικόνα 3, υποδηλώνει τη μεταβλητότητα της επίδρασης του χαρακτηριστικού σε διαφορετικές περιπτώσεις. Χαρακτηριστικά με μεγάλο εύρος τιμών SHAP επηδρούν με διαφορετικό τρόπο ανάλογα με το πλαίσιο και τις τιμές των άλλων χαρακτηριστικών. Η παρουσία «ουρών» στα violin plots υποδηλώνει την ύπαρξη ακραίων περιπτώσεων όπου ένα χαρακτηριστικό έχει ιδιαίτερα μεγάλη θετική ή αρνητική επίδραση. Αυτό αποκαλύπτει την πολυπλοκότητα των αλληλεπιδράσεων μεταξύ των παραμέτρων και την ικανότητα του νευρωνικού δικτύου να συλλαμβάνει μη γραμμικές σχέσεις.
Το διάγραμμα σημαντικότητας χαρακτηριστικών (Εικόνα 4) παρουσιάζει μια σαφή κατάταξη των πέντε παραμέτρων εισόδου με βάση τη μέση απόλυτη τιμή SHAP. Η κατάταξη αυτή αποκαλύπτει ποιες παράμετροι έχουν τη μεγαλύτερη επίδραση στην πρόβλεψη της θεμελιώδους περιόδου, ανεξάρτητα από την κατεύθυνση της επίδρασης (θετική ή αρνητική). Από την Εικόνα 4 προκύπτει ότι τα τρία πιο σημαντικά χαρακτηριστικά είναι ο αριθμός των ορόφων, το μήκος των ανοιγμάτων, και η δυσκαμψία των τοιχοπληρώσεων. Αυτές οι παράμετροι παρουσιάζουν τις υψηλότερες μέσες απόλυτες τιμές SHAP, υποδεικνύοντας ότι έχουν την πιο καθοριστική επίδραση στον προσδιορισμό της θεμελιώδους περιόδου.
Η κατάταξη που προκύπτει από την Εικόνα 4 συμφωνεί σε μεγάλο βαθμό με τις φυσικές προσδοκίες και τη βιβλιογραφία. Ο αριθμός των ορόφων είναι γνωστό ότι αποτελεί τον κυριότερο παράγοντα που επηρεάζει τη θεμελιώδη περίοδο, καθώς το ύψος της κατασκευής είναι η βασική παράμετρος στις περισσότερες εμπειρικές εξισώσεις (όπως η εξίσωση του Eurocode 8: $T_1 = 0.075 \times H^{0.75}$). Το μήκος των ανοιγμάτων επηρεάζει τη δυσκαμψία του φορέα και κατά συνέπεια την περίοδο ταλάντωσης. Η δυσκαμψία των τοιχοπληρώσεων έχει τεκμηριωθεί στη βιβλιογραφία (Asteris et al., 2016) ως σημαντική παράμετρος που μπορεί να μειώσει σημαντικά την περίοδο ταλάντωσης σε σχέση με τον γυμνό φορέα. Ο αριθμός των ανοιγμάτων και το ποσοστό ανοιγμάτων εμφανίζουν χαμηλότερη σημαντικότητα, αλλά παραμένουν σημαντικοί παράγοντες που επηρεάζουν τη συνολική δυσκαμψία της κατασκευής.
Τα αποτελέσματα από την Εικόνα 4 έχουν σημαντικές πρακτικές επιπτώσεις. Οι μηχανικοί που επιθυμούν να εκτιμήσουν ή να ελέγξουν τη θεμελιώδη περίοδο μιας κατασκευής θα πρέπει να δώσουν ιδιαίτερη προσοχή στα τρία πιο σημαντικά χαρακτηριστικά: τον αριθμό των ορόφων, το μήκος των ανοιγμάτων, και τη δυσκαμψία των τοιχοπληρώσεων. Η ακριβής εκτίμηση αυτών των παραμέτρων είναι κρίσιμη για την αξιόπιστη πρόβλεψη της περιόδου. Επιπλέον, το γεγονός ότι το μοντέλο αναγνωρίζει τη σημαντικότητα των τοιχοπληρώσεων υπογραμμίζει την ανάγκη να μην αγνοούνται αυτά τα στοιχεία στην ανάλυση, όπως συχνά συμβαίνει στην απλοποιημένη πρακτική. Η παραμελημένη μοντελοποίηση των τοιχοπληρώσεων μπορεί να οδηγήσει σε σημαντικές αποκλίσεις στην εκτίμηση της θεμελιώδους περιόδου.
Με βάση την ανάλυση των τεσσάρων διαγραμμάτων (Εικόνες 1-4), το νευρωνικό δίκτυο που αναπτύχθηκε επιτυγχάνει εξαιρετική απόδοση στην πρόβλεψη της θεμελιώδους περιόδου πλαισιακών κατασκευών από οπλισμένο σκυρόδεμα με τοιχοπληρώσεις. Η καμπύλη εκπαίδευσης (Εικόνα 1) επιβεβαιώνει τη σταθερή και επιτυχημένη σύγκλιση του μοντέλου, ενώ το διάγραμμα προβλέψεων (Εικόνα 2) αποδεικνύει την υψηλή ακρίβεια με συντελεστές R² που πλησιάζουν τη μονάδα. Το μοντέλο όχι μόνο παρέχει ακριβείς προβλέψεις, αλλά μέσω της ανάλυσης SHAP (Εικόνες 3 και 4) προσφέρει επίσης διαφάνεια και ερμηνευσιμότητα, επιτρέποντας την κατανόηση των φυσικών σχέσεων που έχει μάθει.
Η προσέγγιση που υιοθετήθηκε παρουσιάζει σημαντικά πλεονεκτήματα έναντι παραδοσιακών εμπειρικών μεθόδων. Από τις Εικόνες 1-4 προκύπτει ότι το μοντέλο μπορεί να συλλάβει πολύπλοκες μη γραμμικές σχέσεις μεταξύ των παραμέτρων εισόδου και της θεμελιώδους περιόδου, κάτι που δεν είναι εύκολο με απλές εμπειρικές εξισώσεις. Η ανάλυση SHAP (Εικόνες 3 και 4) αποκαλύπτει όχι μόνο ποιες παράμετροι είναι σημαντικές, αλλά και πώς αυτές αλληλεπιδρούν μεταξύ τους σε διαφορετικά πλαίσια. Επιπλέον, η χρήση της βάσης FP4026 με 4026 αναλυτικά υπολογισμένες περιπτώσεις διασφαλίζει ότι το μοντέλο έχει εκπαιδευτεί σε αξιόπιστα δεδομένα που προέρχονται από λεπτομερείς αναλύσεις πεπερασμένων στοιχείων.
Παρά την εξαιρετική απόδοση που καταγράφηκε, υπάρχουν ορισμένοι περιορισμοί που πρέπει να αναγνωριστούν. Από την Εικόνα 2 παρατηρήθηκαν μικρές συστηματικές αποκλίσεις σε ακραίες τιμές περιόδου, υποδεικνύοντας ότι το μοντέλο ενδέχεται να έχει μειωμένη ακρίβεια σε περιπτώσεις που βρίσκονται στα άκρα της κατανομής των δεδομένων. Επίσης, το μοντέλο είναι εκπαιδευμένο αποκλειστικά στη βάση FP4026, που αφορά συγκεκριμένες γεωμετρικές διαμορφώσεις και παραμέτρους (1-7 όροφοι, 1-5 ανοίγματα, συγκεκριμένα εύρη μηκών και δυσκαμψιών). Η γενίκευση σε κατασκευές με χαρακτηριστικά εκτός αυτών των ορίων δεν έχει επαληθευτεί. Επιπλέον, η βάση FP4026 αφορά κανονικές κατασκευές χωρίς ιδιαιτερότητες (π.χ. ασυμμετρίες, μαλακούς ορόφους), και το μοντέλο δεν μπορεί να αντιμετωπίσει τέτοιες περιπτώσεις. Τέλος, από την Εικόνα 1 φαίνεται ότι η εκπαίδευση για 1000 εποχές ήταν επαρκής, αλλά για μελλοντικές εφαρμογές θα μπορούσαν να διερευνηθούν πιο προηγμένες τεχνικές όπως early stopping ή learning rate scheduling για βελτιστοποίηση της διαδικασίας.
Τεχνητή Νοημοσύνη (Artificial Intelligence - AI) Η Τεχνητή Νοημοσύνη είναι ο ευρύτερος κλάδος της πληροφορικής που ασχολείται με την ανάπτυξη υπολογιστικών συστημάτων ικανών να εκτελούν εργασίες που τυπικά απαιτούν ανθρώπινη νοημοσύνη. Στο πλαίσιο της παρούσας εργασίας, η ΤΝ χρησιμοποιείται για την προσομοίωση της διαδικασίας εκτίμησης της θεμελιώδους περιόδου, μαθαίνοντας από δεδομένα αντί να ακολουθεί ρητούς κανόνες προγραμματισμού.
Μηχανική Μάθηση (Machine Learning - ML) Η Μηχανική Μάθηση αποτελεί υποκατηγορία της Τεχνητής Νοημοσύνης και εστιάζει στην ανάπτυξη αλγορίθμων που βελτιώνονται αυτόματα μέσω της εμπειρίας και της χρήσης δεδομένων. Αντί να προγραμματιστεί ρητά για κάθε πιθανή περίπτωση, το σύστημα "εκπαιδεύεται" σε ένα μεγάλο σύνολο παραδειγμάτων (όπως η βάση FP4026) για να αναγνωρίζει μοτίβα και να κάνει προβλέψεις σε νέα, άγνωστα δεδομένα.
Νευρωνικά Δίκτυα (Neural Networks) Τα Νευρωνικά Δίκτυα είναι υπολογιστικά μοντέλα εμπνευσμένα από τη βιολογική λειτουργία του ανθρώπινου εγκεφάλου. Αποτελούνται από διασυνδεδεμένους κόμβους (νευρώνες) οργανωμένους σε επίπεδα, οι οποίοι επεξεργάζονται πληροφορίες μεταδίδοντας σήματα μεταξύ τους. Είναι εξαιρετικά ικανά στην εκμάθηση μη γραμμικών σχέσεων και πολύπλοκων μοτίβων, καθιστώντας τα ιδανικά για την πρόβλεψη της θεμελιώδους περιόδου σε σύνθετες κατασκευές.
Βαθιά Μάθηση (Deep Learning) Η Βαθιά Μάθηση είναι μια εξειδικευμένη κατηγορία μηχανικής μάθησης που βασίζεται σε τεχνητά νευρωνικά δίκτυα με πολλά κρυφά επίπεδα (εξ ου και ο όρος "βαθιά"). Αυτή η αρχιτεκτονική επιτρέπει στο μοντέλο να μαθαίνει ιεραρχικές αναπαραστάσεις των δεδομένων, εξάγοντας αυτόματα χαρακτηριστικά υψηλότερου επιπέδου από τα πρωτογενή δεδομένα εισόδου.
Ερμηνεύσιμη Τεχνητή Νοημοσύνη (Explainable AI - XAI) Η Ερμηνεύσιμη Τεχνητή Νοημοσύνη αναφέρεται σε μεθόδους και τεχνικές που καθιστούν τα αποτελέσματα των συστημάτων ΤΝ κατανοητά στους ανθρώπους. Σε αντίθεση με τα μοντέλα "μαύρου κουτιού", το XAI στοχεύει να εξηγήσει το "γιατί" πίσω από μια συγκεκριμένη πρόβλεψη, κάτι που είναι κρίσιμο στη μηχανική για την εμπιστοσύνη και την επαλήθευση των αποτελεσμάτων.
Random Forest Ο αλγόριθμος Random Forest είναι μια μέθοδος συνδυαστικής μάθησης (ensemble learning) που λειτουργεί κατασκευάζοντας ένα πλήθος δέντρων απόφασης κατά την εκπαίδευση. Για προβλήματα παλινδρόμησης, η τελική πρόβλεψη προκύπτει από τον μέσο όρο των προβλέψεων όλων των επιμέρους δέντρων, προσφέροντας υψηλή ακρίβεια και ανθεκτικότητα στην υπερπροσαρμογή.
Gradient Boosting (LightGBM, XGBoost, CatBoost) Το Gradient Boosting είναι μια τεχνική μηχανικής μάθησης που παράγει ένα μοντέλο πρόβλεψης με τη μορφή ενός συνόλου ασθενών μοντέλων πρόβλεψης, συνήθως δέντρων απόφασης. Χτίζει το μοντέλο σταδιακά, με κάθε νέο δέντρο να προσπαθεί να διορθώσει τα σφάλματα των προηγούμενων. Υλοποιήσεις όπως το XGBoost και το LightGBM προσφέρουν βελτιστοποιημένη ταχύτητα και απόδοση.
Support Vector Regression (SVR) Η Support Vector Regression είναι μια προσαρμογή των Support Vector Machines (SVM) για προβλήματα παλινδρόμησης. Στόχος της είναι να βρει μια συνάρτηση που αποκλίνει από τις πραγματικές τιμές το πολύ κατά μια ποσότητα ε για όλα τα δεδομένα εκπαίδευσης, ενώ ταυτόχρονα είναι όσο το δυνατόν πιο επίπεδη. Είναι ιδιαίτερα αποτελεσματική σε χώρους υψηλών διαστάσεων.
Multilayer Perceptron (MLP) Το Multilayer Perceptron είναι μια κατηγορία εμπροσθοδρόμου τεχνητού νευρωνικού δικτύου (feedforward ANN). Αποτελείται από τουλάχιστον τρία επίπεδα κόμβων: ένα επίπεδο εισόδου, ένα κρυφό επίπεδο και ένα επίπεδο εξόδου. Κάθε κόμβος, εκτός από τους κόμβους εισόδου, είναι ένας νευρώνας που χρησιμοποιεί μια μη γραμμική συνάρτηση ενεργοποίησης, επιτρέποντας την επίλυση μη γραμμικά διαχωρίσιμων προβλημάτων.
K-Nearest Neighbors (KNN) Ο αλγόριθμος K-Nearest Neighbors είναι μια απλή, μη παραμετρική μέθοδος που χρησιμοποιείται για ταξινόμηση και παλινδρόμηση. Η πρόβλεψη για ένα νέο σημείο βασίζεται στον μέσο όρο των τιμών των 'k' πλησιέστερων γειτόνων του στο σύνολο εκπαίδευσης, βασιζόμενη στην υπόθεση ότι παρόμοια δεδομένα βρίσκονται κοντά στον χώρο των χαρακτηριστικών.
Ridge, Lasso & ElasticNet Regression Αυτές είναι μέθοδοι γραμμικής παλινδρόμησης που ενσωματώνουν όρους κανονικοποίησης (regularization) για την αποφυγή της υπερπροσαρμογής. Η Ridge προσθέτει ποινή L2 (τετράγωνο μεγέθους συντελεστών), η Lasso προσθέτει ποινή L1 (απόλυτη τιμή συντελεστών) που μπορεί να μηδενίσει συντελεστές κάνοντας επιλογή χαρακτηριστικών, και η ElasticNet συνδυάζει και τις δύο.
Ensemble Learning Η Ensemble Learning (Συνδυαστική Μάθηση) είναι μια διαδικασία κατά την οποία πολλαπλά μοντέλα μηχανικής μάθησης συνδυάζονται στρατηγικά για την επίλυση ενός συγκεκριμένου υπολογιστικού προβλήματος. Ο στόχος είναι η δημιουργία ενός ισχυρότερου προγνωστικού μοντέλου που έχει καλύτερη απόδοση γενίκευσης από ό,τι θα είχε οποιοδήποτε από τα επιμέρους μοντέλα μόνο του.
Backpropagation (Οπισθοδιάδοση) Η Οπισθοδιάδοση είναι ο θεμελιώδης αλγόριθμος για την εκπαίδευση νευρωνικών δικτύων. Υπολογίζει την κλίση της συνάρτησης απώλειας ως προς τα βάρη του δικτύου, διαδίδοντας το σφάλμα από την έξοδο προς την είσοδο. Αυτό επιτρέπει την προσαρμογή των βαρών με τρόπο που ελαχιστοποιεί το σφάλμα πρόβλεψης.
Overfitting (Υπερπροσαρμογή) Η Υπερπροσαρμογή συμβαίνει όταν ένα μοντέλο μαθαίνει τα δεδομένα εκπαίδευσης τόσο καλά (συμπεριλαμβανομένου του θορύβου) που χάνει την ικανότητα να γενικεύει σε νέα δεδομένα. Στην εργασία, αυτό ελέγχεται συγκρίνοντας την απόδοση μεταξύ των συνόλων εκπαίδευσης και ελέγχου και χρησιμοποιώντας τεχνικές κανονικοποίησης.
Feature Importance (Σημαντικότητα Χαρακτηριστικών) Η Σημαντικότητα Χαρακτηριστικών αναφέρεται σε τεχνικές που αποδίδουν μια βαθμολογία στις μεταβλητές εισόδου με βάση το πόσο χρήσιμες είναι για την πρόβλεψη της μεταβλητής στόχου. Αυτό βοηθά στην κατανόηση των δεδομένων, στην επιλογή μοντέλου και στη βελτίωση της ερμηνευσιμότητας.
Data Leakage (Διαρροή Πληροφορίας) Η Διαρροή Πληροφορίας συμβαίνει όταν δεδομένα από το σύνολο ελέγχου χρησιμοποιούνται κατά λάθος κατά τη διαδικασία εκπαίδευσης του μοντέλου (π.χ. κατά την κανονικοποίηση). Αυτό οδηγεί σε υπερβολικά αισιόδοξες εκτιμήσεις απόδοσης που δεν ανταποκρίνονται στην πραγματικότητα όταν το μοντέλο εφαρμοστεί σε πραγματικά νέα δεδομένα.
Cross-validation (Διασταυρούμενη Επικύρωση) Η Διασταυρούμενη Επικύρωση είναι μια τεχνική επαναδειγματοληψίας που χρησιμοποιείται για την αξιολόγηση μοντέλων μηχανικής μάθησης σε περιορισμένο δείγμα δεδομένων. Η μέθοδος k-fold χωρίζει τα δεδομένα σε k υποσύνολα και εκπαιδεύει το μοντέλο k φορές, χρησιμοποιώντας κάθε φορά διαφορετικό υποσύνολο για έλεγχο και τα υπόλοιπα για εκπαίδευση.
Συναρτήσεις Ενεργοποίησης (Activation Functions) Οι συναρτήσεις ενεργοποίησης καθορίζουν την έξοδο ενός νευρώνα δεδομένης μιας εισόδου ή ενός συνόλου εισόδων. Εισάγουν μη γραμμικότητες στο δίκτυο, επιτρέποντάς του να μαθαίνει πολύπλοκες σχέσεις. Κοινές συναρτήσεις περιλαμβάνουν τη ReLU (Rectified Linear Unit), την Tanh (Υπερβολική Εφαπτομένη) και τη Sigmoid.
Βελτιστοποιητές (Optimizers) Οι Βελτιστοποιητές είναι αλγόριθμοι ή μέθοδοι που χρησιμοποιούνται για την αλλαγή των ιδιοτήτων του νευρωνικού δικτύου, όπως τα βάρη και ο ρυθμός μάθησης, με σκοπό τη μείωση των απωλειών. Ο Adam (Adaptive Moment Estimation) είναι ένας δημοφιλής βελτιστοποιητής που προσαρμόζει τον ρυθμό μάθησης για κάθε παράμετρο ξεχωριστά.
Συνάρτηση Απώλειας (Loss Function) Η Συνάρτηση Απώλειας ποσοτικοποιεί το πόσο καλά το μοντέλο προβλέπει την αναμενόμενη έξοδο. Στην περίπτωση της παλινδρόμησης, το Μέσο Τετραγωνικό Σφάλμα (MSE) είναι μια κοινή επιλογή, υπολογίζοντας τον μέσο όρο των τετραγώνων των διαφορών μεταξύ των προβλεπόμενων και των πραγματικών τιμών.
Συντελεστής Προσδιορισμού (R²) Ο R² είναι μια στατιστική μετρική που αντιπροσωπεύει το ποσοστό της διακύμανσης της εξαρτημένης μεταβλητής που εξηγείται από τις ανεξάρτητες μεταβλητές στο μοντέλο παλινδρόμησης. Τιμές κοντά στο 1 υποδηλώνουν ότι το μοντέλο προσαρμόζεται πολύ καλά στα δεδομένα.
Μέσο Απόλυτο Σφάλμα (MAE) Το MAE (Mean Absolute Error) είναι ο μέσος όρος της απόλυτης διαφοράς μεταξύ των προβλεπόμενων και των πραγματικών τιμών. Παρέχει μια άμεση ένδειξη του μέσου σφάλματος πρόβλεψης στις ίδιες μονάδες με την εξαρτημένη μεταβλητή.
Ρίζα Μέσου Τετραγωνικού Σφάλματος (RMSE) Το RMSE (Root Mean Squared Error) είναι η τετραγωνική ρίζα του μέσου όρου των τετραγωνικών διαφορών μεταξύ πρόβλεψης και πραγματικότητας. Λόγω του τετραγωνισμού, το RMSE τιμωρεί τα μεγάλα σφάλματα περισσότερο από το MAE, καθιστώντας το χρήσιμο όταν τα μεγάλα σφάλματα είναι ιδιαίτερα ανεπιθύμητα.
PyTorch Το PyTorch είναι μια βιβλιοθήκη μηχανικής μάθησης ανοιχτού κώδικα που χρησιμοποιείται ευρέως για εφαρμογές όπως η όραση υπολογιστών και η επεξεργασία φυσικής γλώσσας. Παρέχει ευελιξία και ταχύτητα, επιτρέποντας τον εύκολο ορισμό και την εκπαίδευση σύνθετων νευρωνικών δικτύων με χρήση GPU.
Scikit-learn Το Scikit-learn είναι μια βιβλιοθήκη για τη γλώσσα προγραμματισμού Python που παρέχει απλά και αποδοτικά εργαλεία για ανάλυση δεδομένων και μηχανική μάθηση. Περιλαμβάνει υλοποιήσεις για πληθώρα αλγορίθμων ταξινόμησης, παλινδρόμησης και ομαδοποίησης, καθώς και εργαλεία προεπεξεργασίας.
SHAP (SHapley Additive exPlanations) Το SHAP είναι μια προσέγγιση της θεωρίας παιγνίων για την εξήγηση της εξόδου οποιουδήποτε μοντέλου μηχανικής μάθησης. Συνδέει τη βέλτιστη κατανομή πίστωσης με τοπικές εξηγήσεις χρησιμοποιώντας τις κλασικές τιμές Shapley, επιτρέποντας την κατανόηση της συμβολής κάθε χαρακτηριστικού σε μια συγκεκριμένη πρόβλεψη.
Scalers (MaxAbsScaler, StandardScaler) Οι Scalers είναι εργαλεία προεπεξεργασίας που χρησιμοποιούνται για την κανονικοποίηση του εύρους των ανεξάρτητων μεταβλητών ή χαρακτηριστικών των δεδομένων. Ο MaxAbsScaler, για παράδειγμα, κλιμακώνει κάθε χαρακτηριστικό με τη μέγιστη απόλυτη τιμή του, διατηρώντας το πρόσημο και τη δομή των αραιών δεδομένων.
Θεμελιώδης Περίοδος (Fundamental Period) Η Θεμελιώδης Περίοδος είναι ο χρόνος που απαιτείται για να ολοκληρώσει μια κατασκευή έναν πλήρη κύκλο ταλάντωσης στην πρώτη (κύρια) ιδιομορφή της. Είναι μια κρίσιμη παράμετρος στον αντισεισμικό σχεδιασμό, καθώς καθορίζει το πώς η κατασκευή θα ανταποκριθεί στις σεισμικές δονήσεις και τα φασματικά μεγέθη σχεδιασμού.
Πλαισιακές Κατασκευές (Frame Structures) Οι Πλαισιακές Κατασκευές είναι δομικά συστήματα που αποτελούνται από έναν συνδυασμό δοκών και υποστυλωμάτων συνδεδεμένων μεταξύ τους για να αντιστέκονται σε φορτία. Στην παρούσα εργασία, εξετάζονται πλαίσια από οπλισμένο σκυρόδεμα, τα οποία είναι ο πιο διαδεδομένος τύπος κατασκευής στην Ελλάδα.
Τοιχοπληρώσεις (Masonry Infills) Οι Τοιχοπληρώσεις είναι οι τοίχοι από οπτοπλινθοδομές που γεμίζουν τα ανοίγματα μεταξύ των δοκών και των υποστυλωμάτων ενός πλαισίου. Αν και συχνά θεωρούνται μη φέροντα στοιχεία, επηρεάζουν σημαντικά τη δυσκαμψία, την αντοχή και τη δυναμική συμπεριφορά της κατασκευής κατά τη διάρκεια ενός σεισμού.
Ισοδύναμος Θλιβόμενος Διαγώνιος Ελκυστήρας Ο Ισοδύναμος Θλιβόμενος Διαγώνιος Ελκυστήρας είναι ένα μακρο-μοντέλο που χρησιμοποιείται για την προσομοίωση της συμπεριφοράς των τοιχοπληρώσεων. Αντικαθιστά το πάνελ της τοιχοποιίας με μια διαγώνια ράβδο που λειτουργεί μόνο σε θλίψη, επιτρέποντας την απλοποιημένη αλλά ακριβή ανάλυση της αλληλεπίδρασης πλαισίου-τοιχοποιίας.
Αριθμός Ορόφων Ο Αριθμός Ορόφων καθορίζει το συνολικό ύψος της κατασκευής και είναι άμεσα συνδεδεμένος με τη μάζα και την ευκαμψία της. Γενικά, η αύξηση του αριθμού των ορόφων οδηγεί σε αύξηση της θεμελιώδους περιόδου ταλάντωσης.
Ποσοστό Ανοιγμάτων Τοιχοποιίας Το Ποσοστό Ανοιγμάτων αναφέρεται στο τμήμα της επιφάνειας ενός τοίχου πλήρωσης που καταλαμβάνεται από ανοίγματα (παράθυρα, πόρτες). Η παρουσία ανοιγμάτων μειώνει τη δυσκαμψία της τοιχοποιίας και επηρεάζει την ικανότητά της να λειτουργεί ως διαγώνιος ελκυστήρας.
Δυσκαμψία Τοιχοποιίας Η Δυσκαμψία Τοιχοποιίας είναι ένα μέτρο της αντίστασης που προβάλλει η τοιχοπλήρωση στην παραμόρφωση. Εξαρτάται από το υλικό της τοιχοποιίας, το πάχος του τοίχου και την ποιότητα κατασκευής, και παίζει καθοριστικό ρόλο στη συνολική πλευρική δυσκαμψία του κτιρίου.
Οπλισμένο Σκυρόδεμα (Reinforced Concrete) Το Οπλισμένο Σκυρόδεμα είναι ένα σύνθετο υλικό που συνδυάζει σκυρόδεμα (ανθεκτικό σε θλίψη) και χάλυβα οπλισμού (ανθεκτικό σε εφελκυσμό). Η κατηγορία αντοχής (π.χ. C25/30) και τα χαρακτηριστικά του χάλυβα (π.χ. B500c) καθορίζουν τη μηχανική συμπεριφορά των μελών του πλαισίου.
Μέτρο Ελαστικότητας (Modulus of Elasticity) Το Μέτρο Ελαστικότητας είναι μια μηχανική ιδιότητα που περιγράφει την αντίσταση ενός υλικού στην ελαστική παραμόρφωση όταν ασκείται τάση. Είναι θεμελιώδες για τον υπολογισμό της δυσκαμψίας των δομικών στοιχείων και, κατ' επέκταση, της ιδιοπεριόδου της κατασκευής.
Eurocode 8 (Ευρωκώδικας 8) Ο Ευρωκώδικας 8 είναι το σύνολο των ευρωπαϊκών προτύπων για τον σχεδιασμό κατασκευών για αντοχή σε σεισμό. Παρέχει κανόνες και οδηγίες για την ανάλυση, τη διαστασιολόγηση και την κατασκευή κτιρίων σε σεισμογενείς περιοχές, συμπεριλαμβανομένων εμπειρικών τύπων για την εκτίμηση της ιδιοπεριόδου.
SeismoStruct Το SeismoStruct είναι ένα πακέτο λογισμικού πεπερασμένων στοιχείων ικανό να προβλέπει τη συμπεριφορά πλαισίων χώρου υπό στατικά ή δυναμικά φορτία, λαμβάνοντας υπόψη γεωμετρικές μη γραμμικότητες και ανελαστικότητα υλικών. Χρησιμοποιήθηκε για τη δημιουργία της βάσης δεδομένων FP4026 μέσω αναλυτικών προσομοιώσεων.
Αυτή η ενότητα περιέχει το πλήρες output της εκτέλεσης του προγράμματος μηχανικής μάθησης, συμπεριλαμβανομένης της σύγκρισης με τον Ευρωκώδικα 8.
Program started at: 2025-12-06 22:07:43
============================================================
[Dataset] Loaded successfully
Total samples: 4026
Features: 6
[Features] Selected features:
1. Number of Storeys (-)
2. Number of Spans (-)
3. Length of Spans (m)
4. Opening percentage (%)
5. Masonry wall Stiffness (10^5 kN/m)
[Model] Neural Network Architecture:
Input features: 5
Hidden layers: 3
Neurons per layer: 64
Activation function: relu
Total parameters: 8769
[Training] Started...
Epochs: 2000
Optimizer: Adam (lr=0.001)
Loss function: MSE
[Training] 10% done - Epoch 200/2000, Loss: 0.0071
[Training] 20% done - Epoch 400/2000, Loss: 0.0021
[Training] 30% done - Epoch 600/2000, Loss: 0.0013
[Training] 40% done - Epoch 800/2000, Loss: 0.0010
[Training] 50% done - Epoch 1000/2000, Loss: 0.0008
[Training] 60% done - Epoch 1200/2000, Loss: 0.0007
[Training] 70% done - Epoch 1400/2000, Loss: 0.0007
[Training] 80% done - Epoch 1600/2000, Loss: 0.0006
[Training] 90% done - Epoch 1800/2000, Loss: 0.0006
[Training] 100% done - Epoch 2000/2000, Loss: 0.0005
[Training] 100% - Training completed!
Test Loss: 0.0006
============================================================
COMPARISON: ML MODEL vs EUROCODE 8
============================================================
--- Eurocode 8 Performance ---
EC8 Test R2: 0.5651
EC8 Train R2: 0.5474
EC8 All Data R2: 0.5493
--- ML Model Performance ---
ML Test R2: 0.9990
ML Train R2: 0.9992
ML All Data R2: 0.9991
--- Improvement ---
ML improves R2 (test) by: 99.78%
ML improves R2 (all) by: 99.81%
============================================================
[SHAP] Computing SHAP values (this may take a few minutes)...
[SHAP] SHAP values computed successfully!
[Plotting] Generating figures...
- Figure 1: Training Loss vs. Epoch
- Figure 2: ML Model Predictions vs. True
- Figure 2b: Eurocode 8 Predictions vs. True
- Figure 3: SHAP Violin Plot
- Figure 4: Feature Importance
[Completed] All figures generated successfully!
============================================================
Program completed at: 2025-12-06 22:15:11
============================================================